У нас на графике трапеция. Перемещение в данном случае равна площади под графиком(Если б скорость уходила бы в минус, тогда для рассчётов вектора перемещения нам понадобилось бы вычесть площадь минусовой части V). Площадь трапеции равна полусумме его оснований умноженное на её высоту.
Составим уравнение для пути s за последнюю секунду как разность расстояний, пройденных телом при свободном падении без начальной скорости (υо= 0 ) за время t и за время t - ∆t (по условию ∆t= 1 с): s = gt2/2 - g(t - ∆t)2/2. (1) из этого уравнения находим t : 2s = gt2- g(t - ∆t)2, 2s/g = t2- t2+ 2t∆t - ∆t2 => t = s/g∆t+ ∆t/2. t = 25 м/10 м/с2 ∙1 с + 1/2 с = 3 с. и подставляем его в формулу h = gt2/2. (2) вычислим: h = 10 м/с2∙(3 с)2/2 = 45 м. ответ: 45 м.
300м
Объяснение:
Граф. метод։
У нас на графике трапеция. Перемещение в данном случае равна площади под графиком(Если б скорость уходила бы в минус, тогда для рассчётов вектора перемещения нам понадобилось бы вычесть площадь минусовой части V). Площадь трапеции равна полусумме его оснований умноженное на её высоту.
⇒|S(вектор перемещения)| =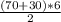
= 300м
Анал. метод։
0) V₀ = 0м/c, V₁ = 6м/c, Δt = 30с
⇒ a₀ = (V₁-V₀)/Δt = 0.2м/c²
⇒ S₀ = a₀Δt²/2 = 90м
1) a₁ = 0м/c²
⇒ S₁ = V₁ × t₁ = 6 × 30 = 180м
2) V₁ = 6м/c V₂ = 0 Δt = 10с
⇒ a₂ = -0.6м/c²
⇒ S₂ = V₁×Δt + a₂Δt²/2 = V₁²/(2×a₂) = 30м
⇒ ∑S = 90 + 180 + 30 = 300м