Наклон плоскости характеризует угол α. Даны три наклонные плоскости с различными углами:
у 1-й плоскости α1=29 градуса(-ов),
у 2-й плоскости α2=49 градуса(-ов),
у 3-й плоскости α3=11 градуса(-ов).
Какую из плоскостей следует использовать, чтобы получить наибольшую экономию силы?
Среднюю скорость катера можно сосчитать по формуле:
\[{\upsilon _{ср}} = \frac{{{S_1} + {S_2}}}{{{t_1} + {t_2}}}\]
Движение на обоих участках было равномерным, поэтому найти время \(t_1\) и \(t_2\) не составит труда.
\[\left\{ \begin{gathered}
{t_1} = \frac{{{S_1}}}{{{\upsilon _1}}} \hfill \\
{t_2} = \frac{{{S_2}}}{{{\upsilon _2}}} \hfill \\
\end{gathered} \right.\]
Так как участки равны по величине \(S_1=S_2=\frac{1}{2}S\), и скорость на первой участке больше скорости на втором в два раза \(\upsilon_1=2\upsilon_2\), то:
\[\left\{ \begin{gathered}
{t_1} = \frac{S}{{2{\upsilon _1}}} = \frac{S}{{4{\upsilon _2}}} \hfill \\
{t_2} = \frac{S}{{2{\upsilon _2}}} \hfill \\
\end{gathered} \right.\]
Подставим выражения для времен \(t_1\) и \(t_2\) в формулу средней скорости.
\[{\upsilon _{ср}} = \frac{S}{{\frac{S}{{4{\upsilon _2}}} + \frac{S}{{2{\upsilon _2 = \frac{S}{{\frac{{3S}}{{4{\upsilon _2 = \frac{{S \cdot 4{\upsilon _2}}}{{3S}} = \frac{{4{\upsilon _2}}}{3}\]
Значит необходимая нам скорость \(\upsilon_2\) определяется по такой формуле.
Найти предельное значение массы груза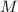
Будем считать, что шар с грузом поднимается достаточно медленно для того, чтобы силой сопротивления воздуха можно было пренебречь. Тогда на шар действует две силы - сила тяжести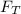
и подъемная сила 
.
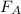Чтобы шар начал подниматься должно выполняться условие:
При этом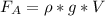
--------(2)
Подставим в (1) вместо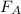
и 
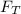выражения (2) и (3):
ответ: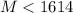
кг