, и значит, в А потенциал ближе к B, чем к С, и в то же время , а значит, в центре потенциал ближе к C, чем к B. Т.е. в А потенциал выше, чем в центре, а значит, из A в центр течёт положительный ток.
Пусть через течёт .
Пусть через течёт , тогда через течёт .
Все дальнейшие выкладки ведутся в системе СИ, в вольтах, амперах и омах, без постоянного их упоминания.
А общее падение напряжения от B к C через A составит:
;
Пусть через течёт , тогда через течёт .
А общее падение напряжения от B к C через центр составит:
;
Получаем уравнение:
;
;
;
(*) ;
На падает напряжение ;
На падает напряжение ;
При этом понятно, что на падение напряжение больше (в центре более низкий потенциал, чем в А) на величину
Отсюда получаем второе уравнение: ;
(**) ;
Решаем систему, вычитая из утроенного (*) одно (**):
;
;
, из (*);
Общее падение напряжения от B к C составляет:
;
Из точки B вытекают токи и ещё ток ;
Общий ток из B в C:
;
Полное сопротивление цепи составит:
;
Ом.
* Если бы ток был направлен в другую сторону, то оказалось бы, что , тогда общий ток должен был бы выражалтья через отрицательный коэффициент от , ну, а поскольку , то, с самого начала, мы выбрали удачное направление для . Хотя, будь он и отрицательным (при других параметрах), это ничего бы принципиально не изменило в решении. Просто в конце концов, мы поделили бы одно алгебраическое выражение с минусом на другое выражение с минусом, и так же получили бы какое-то положительное выражение для общего сопротивления.
Объяснение:
Пусть через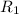 течёт
течёт 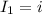 .
.
Пусть через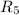 течёт
течёт 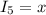 , тогда через
, тогда через 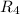 течёт
течёт 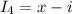 .
.
Все дальнейшие выкладки ведутся в системе СИ, в вольтах, амперах и омах, без постоянного их упоминания.
А общее падение напряжения от B к C через A составит:
Пусть через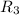 течёт
течёт  , тогда через
, тогда через 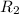 течёт
течёт 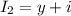 .
.
А общее падение напряжения от B к C через центр составит:
Получаем уравнение:
(*)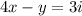 ;
;
На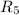 падает напряжение
падает напряжение 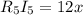 ;
;
На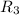 падает напряжение
падает напряжение 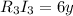 ;
;
При этом понятно, что на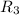 падение напряжение больше (в центре более низкий потенциал, чем в А) на величину
падение напряжение больше (в центре более низкий потенциал, чем в А) на величину 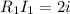
Отсюда получаем второе уравнение: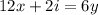 ;
;
(**)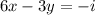 ;
;
Решаем систему, вычитая из утроенного (*) одно (**):
Общее падение напряжения от B к C составляет:
Из точки B вытекают токи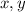 и ещё ток
и ещё ток 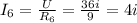 ;
;
Общий ток из B в C:
Полное сопротивление цепи составит:
* Если бы ток был направлен в другую сторону, то оказалось бы, что
был направлен в другую сторону, то оказалось бы, что 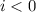 , тогда общий ток
, тогда общий ток 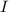 должен был бы выражалтья через отрицательный коэффициент от
должен был бы выражалтья через отрицательный коэффициент от  , ну, а поскольку
, ну, а поскольку 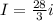 , то, с самого начала, мы выбрали удачное направление для
, то, с самого начала, мы выбрали удачное направление для  . Хотя, будь он и отрицательным (при других параметрах), это ничего бы принципиально не изменило в решении. Просто в конце концов, мы поделили бы одно алгебраическое выражение с минусом на другое выражение с минусом, и так же получили бы какое-то положительное выражение для общего сопротивления.
. Хотя, будь он и отрицательным (при других параметрах), это ничего бы принципиально не изменило в решении. Просто в конце концов, мы поделили бы одно алгебраическое выражение с минусом на другое выражение с минусом, и так же получили бы какое-то положительное выражение для общего сопротивления.