где Е1(п/к)- это потенциальная/кинетическая энергия тела в момент времени когда отношение энергий равно 3
-------
в момент времени когда тело было брошено его потенциальная энергия(Е0(п)) равна нулю и тело обладало лишь кинетической энергией(Е0(к)). из закона сохранения энергии:
Слишком много данных в этой задаче. Можно, конечно, решить её, воспользовавшись данными о планете, но из-за мелких чисел тут будет либо грубое округление, либо много лишних рассчётов, поэтому т.к. нам известны путь, пройденный телом (высота падения) и время, за которое тело этот путь (упало), то подставим просто значения в формулу
a =
Т.к. путь равен 0,8м, а время - 1,049 сек, то подставляем значения и вычисляем на калькуляторе, а ответ округляем до тысячных и получаем 1,454 м/с²
Объяснение:
E(потенциальная)=mgh
E(кинетическая)=
где m-масса тела
v-скорость тела
h-высота тела относительно высоты броска
g-гравитационная постоянная
-------
из условия:
E1(п)/Е1(к)=3 =>
=> Е1(к)=Е1(п)/3
где Е1(п/к)- это потенциальная/кинетическая энергия тела в момент времени когда отношение энергий равно 3
-------
в момент времени когда тело было брошено его потенциальная энергия(Е0(п)) равна нулю и тело обладало лишь кинетической энергией(Е0(к)). из закона сохранения энергии:
Е0(к)=Е1(к)+Е1(п)
Е0(к)=Е1(п)+Е1(п)/3=(4/3)Е1(п)
Е1(п)=(3/4)Е0(к)
mgh=(3/8)mv^2
h=(3/8g)v^2
осталось лишь подставить числа:
из условия v=49/10 м/с.
h=7203/8000 метра
g ≈ 1,454 м/с²
Объяснение:
Слишком много данных в этой задаче. Можно, конечно, решить её, воспользовавшись данными о планете, но из-за мелких чисел тут будет либо грубое округление, либо много лишних рассчётов, поэтому т.к. нам известны путь, пройденный телом (высота падения) и время, за которое тело этот путь (упало), то подставим просто значения в формулу
a =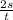
Т.к. путь равен 0,8м, а время - 1,049 сек, то подставляем значения и вычисляем на калькуляторе, а ответ округляем до тысячных и получаем 1,454 м/с²