Найти расстояние между двумя пущенными из пушки под углом к горизонту α = 45° и α = 15° с начальной скоростью 32 (м/с). под расстоянием поднимается, расстояние между после падения.
Запишем формулу напряжённости электрического поля , где q₀ - величина заряда (Кл), R - расстояние между зарядами (м), k - коэффициент пропорциональности (k = 9·10⁹ Н·м² / Кл²), е - диэлектрическая проницаемость.
Запишем формулу потенциала точечного заряда , где q - величина заряда (Кл), R - расстояние между зарядами (м), k - коэффициент пропорциональности (k = 9·10⁹ Н·м² / Кл²).
Выразим напржяённость электрического поля через потенциал точечного заряда:
. В системе СИ 5 нКл = 5*10⁻⁹ Кл. Подставляем числовые занчения и вычисляем искомую величину диэлектрической проницаемости:
№3.
При паралельном соеденении конденсаторов:
Как видим ёмкости складываются. Для данного случая:
Подставим и вычислим искомую величину ёмкости второго заряда:
№4.
По формуле напряжённости электрического поля , где F - действующая сила (Н), q - величина заряда (Кл). Где действующую силу распишим
по формуле второго закона Ньютона , где m - масса тела (кг), а - ускорение тела (м/с²). Масса электрона . Подставим в формулу закона Ньютона: . В системе СИ: 0,8 Тм/с = 0,8*10¹² м/с.
№1. Решение во вложении..!
№2.
Запишем формулу напряжённости электрического поля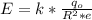
, где q₀ - величина заряда (Кл), R - расстояние между зарядами (м), k - коэффициент пропорциональности (k = 9·10⁹ Н·м² / Кл²), е - диэлектрическая проницаемость.
Запишем формулу потенциала точечного заряда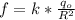
, где q - величина заряда (Кл), R - расстояние между зарядами (м), k - коэффициент пропорциональности (k = 9·10⁹ Н·м² / Кл²).
Выразим напржяённость электрического поля через потенциал точечного заряда:
Выразим искомую величину диэлектрической проницаемости:
№3.
При паралельном соеденении конденсаторов: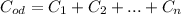
Как видим ёмкости складываются. Для данного случая: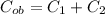
Подставим и вычислим искомую величину ёмкости второго заряда:
№4.
По формуле напряжённости электрического поля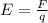
, где F - действующая сила (Н), q - величина заряда (Кл). Где действующую силу распишим
по формуле второго закона Ньютона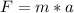
, где m - масса тела (кг), а - ускорение тела (м/с²). Масса электрона 
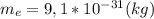. Подставим в формулу закона Ньютона: 
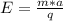. В системе СИ: 0,8 Тм/с = 0,8*10¹² м/с.
Заряд электрона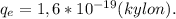
. Подставляем и вычисляем:
1. ρ=1000 кг/м³
g=10 м/с²
h=12 м
насос должен создавать давление p=ρ·g·h=1000·10·12=120000 Па =120 кПа
2. P=gPh
P=10H/кг×1036кг/м³×0,7м=7252 Па
7252 Па = 7,252 кПа
Округляем 7,25 кПа
3. 47,38 МПа= 47380000 Па
p=ρgh
h=p/(ρg)=47380000/(1030•10)=4600 м= 4,6 км
4. Дано:
g - 10 Н/кг
ρ воды - 1000 кг/м^3
h1 - 249 м
h2 - 20 м
p1 - ?
p2 - ?
S (разность давлений) - ?
p=ρgh >>>
р1=ρgh1=1000*10*249=2 490 000 Па
р2=ρgh2=1000*10*20=200 000 Па
S=p1-p2=2 490 000 - 200 000 = 2 290 000 Па
ответ: отличаются на 2 290 000 Па