найти заряд, который проводником с сопротивлением 3 Ом с условием равномерного повышения напряжения на концах проводника от 2 В до 4 В, в течение 20 с.
Интересная задача, решим ее графически, без интегралов. Изобразим график изменения тока со временем. Ток, по закону Ома, меняется с величины А до величины А. Очевидно, что заряд по проводнику, равен по величине площади под графиком тока. Найдем площадь заштрихованной трапеции (полусумма оснований, умноженная на высоту)
Объяснение: В начале напряжение равно 2В, сопротивление = 3 ом, значит, по закону Ома для участка цепи : I=U/R, то есть ток равен 2В/3 Ом = 2/3 А. В конце же, ток равен 4В/3 Ом = 4/3 А. Заряд равен частному изменения тока на время, то есть , (I2 - I1)/t = (4/3 - 2/3)/20с =1/30 = 0,033Кл.
20 Кл
Объяснение:
Интересная задача, решим ее графически, без интегралов. Изобразим график изменения тока со временем. Ток, по закону Ома, меняется с величины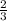 А до величины
А до величины 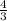 А. Очевидно, что заряд по проводнику, равен по величине площади под графиком тока. Найдем площадь заштрихованной трапеции (полусумма оснований, умноженная на высоту)
А. Очевидно, что заряд по проводнику, равен по величине площади под графиком тока. Найдем площадь заштрихованной трапеции (полусумма оснований, умноженная на высоту)
ответ:0,03 Кл
Объяснение: В начале напряжение равно 2В, сопротивление = 3 ом, значит, по закону Ома для участка цепи : I=U/R, то есть ток равен 2В/3 Ом = 2/3 А. В конце же, ток равен 4В/3 Ом = 4/3 А. Заряд равен частному изменения тока на время, то есть , (I2 - I1)/t = (4/3 - 2/3)/20с =1/30 = 0,033Кл.