Некоторая масса газа с двухатомными молекулами при давлении p1=710 кПа имела объём V1=0,94 м3, а при давлении p2=320 кПа – объём V2=0,82 м3. Переход от первого состояния ко второму был сделан в два этапа: сначала по изобаре, а затем по адиабате. Определить количество поглощённой теплоты Q.
На примере рассмотрим свободное падение тела с начальной скоростью
v
0
под действием силы тяжести за промежуток времени
t
. При направлении оси
O
Y
вертикально вниз импульс силы тяжести
F
т
=
mg
, действующий за время
t
, равняется
m
g
t
. Такой импульс равняется изменению импульса тела:
F
т
t
=
m
g
t
=
Δ
p
=
m
(
v
–
v
0
)
, откуда
v
=
v
0
+
g
t
.
Запись совпадает с кинематической формулой определения скорости равноускоренного движения. По модулю сила не изменяется из всего интервала
t
. Когда она изменяема по величине, тогда формула импульса требует подстановки среднего значения силы
F
с
р
из временного промежутка
t
. Рисунок
1
.
16
.
2
показывает, каким образом определяется импульс силы, которая зависит от времени.
Изменение импульса
Рисунок
1
.
16
.
2
.
Вычисление импульса силы по графику зависимости
F
(
t
)
Необходимо выбрать на временной оси интервал
Δ
t
, видно, что сила
F
(
t
)
практически неизменна. Импульс силы
F
(
t
)
Δ
t
за промежуток времени
Δ
t
будет равняться площади заштрихованной фигуры. При разделении временной оси на интервалы на
Δ
t
i
на промежутке от от
0
до
t
, сложить импульсы всех действующих сил из этих промежутков
Δ
t
i
, тогда суммарный импульс силы будет равняться площади образования при ступенчатой и временной осей.
Применив предел
(
Δ
t
i
→
0
)
, можно найти площадь, которая будет ограничиваться графиком
F
(
t
)
и осью
t
. Использование определения импульса силы по графику применимо с любыми законами, где имеются изменяющиеся силы и время. Данное решение ведет к интегрированию функции
F
(
t
)
из интервала
[
0
;
t
]
.
Рисунок
1
.
16
.
2
показывает импульс силы, находящийся на интервале от
t
1
=
0
с до
t
2
=
10
.
Из формулы получим, что
F
с
р
(
t
2
−
t
1
)
=
1
2
F
m
a
x
(
t
2
−
t
1
)
=
100
Н
⋅
с
=
100
к
г
⋅
м
/
с
.
То есть, из примера видно
F
с
р
=
1
2
F
m
a
x
=
10
Н
.
Объяснение:
1) а = - 0,56 м/с^2
Решение: Переводим скорость и время в СИ. V2 = 20 м/c (*1000:3600) и t = 36 c (*60). Далее воспользуемся формулой ускорения для прямолинейного равноускоренного движения -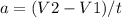 , где V2 = 20 м/с, а V1 = 0 так как мотоциклист остановился. Подставляем значения и считаем.
, где V2 = 20 м/с, а V1 = 0 так как мотоциклист остановился. Подставляем значения и считаем.
2) S = 12,5 м; V1 = 2,5 м/c
Решение: Воспользуемся этой же формулой ускорения -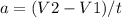 , где V2=0, а V1 неизвестно. Выразим V1
, где V2=0, а V1 неизвестно. Выразим V1 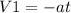 . Так как велосипедист тормозит, ускорение направлено против ОХ, то есть равно a = -0,25 м/с^2. Подставляем значения и считаем. Чтобы найти путь, пройденный велосипедистом при торможении воспользуемся формулой связи перемещения тела с его начальной и конечной скорости при прямолинейном равноускоренном движении -
. Так как велосипедист тормозит, ускорение направлено против ОХ, то есть равно a = -0,25 м/с^2. Подставляем значения и считаем. Чтобы найти путь, пройденный велосипедистом при торможении воспользуемся формулой связи перемещения тела с его начальной и конечной скорости при прямолинейном равноускоренном движении - 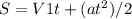 . Подставляем значения и считаем.
. Подставляем значения и считаем.
3) S = 591 м
Решение: Переводим скорость и время в СИ. V1 = 20 м/c (*1000:3600) и t = 30c (*60). Так как автобус тормозит, ускорение направлено против ОХ, то есть равно a = -0,02 м/с^2. Воспользуемся этой же формулой перемещения -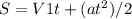 . Подставляем значения и считаем.
. Подставляем значения и считаем.