No 5. Определение силы, действующей на тело, погруженное в жидкость Цель работы: наблюдение за действием выталкивающей силы на погружен- ные в жидкость тела и определение этой силы, Приборы и материалы: динамометр, штатив с муфтой и держателями, два предмета разных размеров, стаканы с водой и водным раствором соли. Указания к выполнению работы: 1. Повторите по учебнику тему «Архимедова сила». 2. Прикрепите динамометр к штативу, подвесьте к нему предмет на нитке. Обуз- начьте и запишите показания динамометра. Это будет весом предмета на воздухе (Р). 3. Поставьте стакан с водой, опускайте муфту и динамометр вниз, пока предмет полностью не погрузится в воду. Обозначьте показатели динамометра и запишите их. Это будет весом предмета в воде (Р). 4. На основе полученных сведений вычислите выталкивающую силу, действу- ющую на предмет (F = Р. – Р.). 5. вместо воды налейте В сосуд раствор соли и снова определите выталкивающую силу действующую на предмет 6 .начертите в тетради следующую таблицу и запишите в неё итоги своих вычислений 7. сделайте выводы ( есть фото таблицы, если можно расписанный ответ очень нужно
кра́сная грани́ца фотоэффе́кта - минимальная частота света , при которой еще возможен внешний фотоэффект, т.е. начальная кинетическая энергия фотоэлектронов больше нуля. частота зависит только от работы выхода электрона: vo=a/hгде a - работы выхода для конкретного фотокатода, а h - постоянная планка. работа выхода a зависит от материала фотокатода и состояния его поверхности. испускание фотоэлектронов начинается сразу же, как только на фотокатод падает свет с частотой . потому что атом из решетки рано или поздно вылетит, т.к. у него есть определенная сила, с которой он держится в решетке
Немного неоднозначная задача, нужно найти кинетическую и потенциальную энергию, хотя не сказано с какого именно положения нужно вести отсчет времени. Я выберу это положение сам.
И еще вопрос, что понимается под амплитудой колебаний? Пусть это будет максимальной высотой подъема тела (#)
По закону сохранения энергии
(*)
где
h - амплитуда, т.е. максимальная высота подъема качели
x(t) - высота качели как ф-я времени
x'(t) - соотв. скорость качели как ф-я времени
(таким образом в правой части имеем потенциальную и кинетическую энергии)
Поставим начальное условие x(0)=0, т.е. пусть в начальный момент времени человек находился в самой нижней точке с макс. кинетической энергией.
Решим ОДУ (*) методом разделения переменных, получим в качестве решения ф-ии
из этих ф-ий выберем ту что с плюсом, т.к. именно ее производная при обращается в нуль, что соответствует моменту остановки качели по достижении макс высоты. Найдем когда именно скорость равна нулю:
отсюда
Стоит отметить, что это решение описывает движение качели лишь на интервале времени от 0 до половины периода. Но этого нам достаточно, ибо требуется найти энергии при t = 1/12 T (где T-период)
Таким образом значение нам теперь известно. Тогда
Значит качели в момент времени были на высоте
Отсюда потенциальная энергия
(Дж)
И кинетическая энергия
(Дж)
(#) Задачу можно рассматривать и как задачу гармонического осциллятора, т.е. с потенциальной энергией вида заместо типичной В этом случае данная в условии задачи частота будет использоваться (чтоб найти омега) В то же время решение ОДУ будет посложнее, функция сведется к тангенсу или чему-то подобному.
Как именно интерпретировать задачу зависит от интерпретации слова амплитуда. Я выбрал самый простой случай и что-то решил, вполне возможно совсем не то, что хотели бы видеть авторы задачи.
кра́сная грани́ца фотоэффе́кта - минимальная частота света , при которой еще возможен внешний фотоэффект, т.е. начальная кинетическая энергия фотоэлектронов больше нуля. частота зависит только от работы выхода электрона: vo=a/hгде a - работы выхода для конкретного фотокатода, а h - постоянная планка. работа выхода a зависит от материала фотокатода и состояния его поверхности. испускание фотоэлектронов начинается сразу же, как только на фотокатод падает свет с частотой . потому что атом из решетки рано или поздно вылетит, т.к. у него есть определенная сила, с которой он держится в решетке
Немного неоднозначная задача, нужно найти кинетическую и потенциальную энергию, хотя не сказано с какого именно положения нужно вести отсчет времени. Я выберу это положение сам.
И еще вопрос, что понимается под амплитудой колебаний? Пусть это будет максимальной высотой подъема тела (#)
По закону сохранения энергии
где
h - амплитуда, т.е. максимальная высота подъема качели
x(t) - высота качели как ф-я времени
x'(t) - соотв. скорость качели как ф-я времени
(таким образом в правой части имеем потенциальную и кинетическую энергии)
Поставим начальное условие x(0)=0, т.е. пусть в начальный момент времени человек находился в самой нижней точке с макс. кинетической энергией.
Решим ОДУ (*) методом разделения переменных, получим в качестве решения ф-ии
из этих ф-ий выберем ту что с плюсом, т.к. именно ее производная при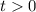 обращается в нуль, что соответствует моменту остановки качели по достижении макс высоты. Найдем когда именно скорость равна нулю:
обращается в нуль, что соответствует моменту остановки качели по достижении макс высоты. Найдем когда именно скорость равна нулю:
отсюда
Стоит отметить, что это решение описывает движение качели лишь на интервале времени от 0 до половины периода. Но этого нам достаточно, ибо требуется найти энергии при t = 1/12 T (где T-период)
Таким образом значение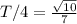 нам теперь известно. Тогда
нам теперь известно. Тогда 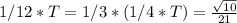
Значит качели в момент времени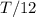 были на высоте
были на высоте 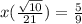
Отсюда потенциальная энергия
И кинетическая энергия
(#) Задачу можно рассматривать и как задачу гармонического осциллятора, т.е. с потенциальной энергией вида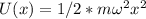 заместо типичной
заместо типичной 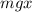 В этом случае данная в условии задачи частота будет использоваться (чтоб найти омега) В то же время решение ОДУ будет посложнее, функция сведется к тангенсу или чему-то подобному.
В этом случае данная в условии задачи частота будет использоваться (чтоб найти омега) В то же время решение ОДУ будет посложнее, функция сведется к тангенсу или чему-то подобному.
Как именно интерпретировать задачу зависит от интерпретации слова амплитуда. Я выбрал самый простой случай и что-то решил, вполне возможно совсем не то, что хотели бы видеть авторы задачи.