км/ч м/с - скорость автобуса на втором участке пути;
с - время, за которое автобус разогнался до скорости, равной 27 км/ч;
с - время движения автобуса с постоянной скоростью, равной 27 км/ч;
с - время торможения автобуса, то есть уменьшения скорости от 27 км/ч до 0.
Необходимо найти: .
Как видно из задачи, общий путь между остановками будет равен пути, потраченном на разгон, пути с постоянной скоростью и пути, с постоянным торможением. Разберем каждый участок пути отдельно.
Путь на первом участке, согласно формуле движения с постоянным ускорением будет иметь вид:
Время нам известно, неизвестно лишь ускорение . Так как начальная скорость м/с, то можем записать:
(1)
Ускорение в данном случае будет иметь вид: , и если , то получаем:
Подставляя в формулу (1) получим:
Можем сразу посчитать:
м. - пройдя расстояние автобус разгонится до скорости 27 км/ч или 7,5 м/с за 5 секунд.
Вторая часть пути, это путь с постоянной скоростью .
На данном участке пути, пройденное расстояние будет иметь вид:
м. - такое расстояние проедет автобус с постоянной скоростью.
Затем, автобус станет тормозить, то есть у нас равнозамедленное движение с постоянным отрицательным ускорением.
Пройденный путь на данном участке будет, согласно формуле равнозамедленного движения:
(2)
В данном случае, так как автобус в итоге затормозит и уменьшит свою скорость до нуля (), то ускорение можно найти согласно формуле:
Если м/с, то ускорение будет равно:
(3)
Тогда подставляя формулу (3) в формулу (2) получим:
Все данные нам известны, подставляем и считаем:
м. - за такое расстояние автобус полностью остановится со скорости м/с за время 8 с.
Теперь, чтобы найти весь путь, пройденный автобусом, сложим , и :
1) Для нахождения силы тока в соленоида определяется вот такая формула из энергий магнитного поля, при этой формулы мы найдем силы тока в соленоида:
- энергия магнитного поля (1)
2) Объемная плотность энергии магнитного поля внутри соленоида определяется по такой формуле именно по такой формуле мы подставим на (1) формулу:
- объемная плотность энергии магнитного поля внутри соленоида (2)
3) Но из формулы (2) нам не известно объем соленоида, но в условий есть длина и площадь, значит мы найдем его, запишем эту формулу и потом мы подставим в формулу (2):
- объем соленоида (3)
4) Следовательно из формулы (1), (2), (3) мы получим общую формулу для нахождения силы тока в соленоиде:
- Сила тока в солинойде
I = √((2×12×10⁻³ Дж/м³ × 60×10⁻⁴ м² × 0,82 м)/0,012 Гн) = √((24×10⁻³ Дж/м³ × 49,2×10⁻⁴ м³)/0,012 Гн) = √((1180,8×10⁻⁷ Дж)/0,012 Гн) = √(98400×10⁻⁷ А²) = √((98400/10⁷) А²) = (√98400)/(√10⁷) А = (20√(246))/(1000√(10)) А × (√10)/(√10) = (20√(2460))/(1000×10) А = (20√(2460))/10000 А ≈ 0,002×49,5984 А ≈ 0,0991968 А ≈ 0,1 А
ответ:
2.
Дано:
Г = 2,5
D = 2,5 Дптр
-----------------------
Найти:
d - ?
Мы находим формулы линзы, именно по такой формуле мы найдем расстояние от линзы до предмета:
Г = f/d - Увеличение линзы
D = 1/F - Оптическая сила линзы
1/F = 1/f + 1/d - Формула линзы, следовательно:
D = 1/f + 1/d ⇒ D = (1/(Г×d)) + 1/d ⇒ D = (1/(Г×d)) + (Г/(Г×d)) ⇒ D = (1+Г)/(Г×d) | × (Г×d) ⇒ D×(Г×d) = 1+Г | : d ⇒ d = (1+Г)/(D×Г) - расстояние от линзы до предмета (4)
d = (1+2,5)/(2,5 Дптр × 2,5) = 3,5/(6,25 Дптр) = 0,56 м
ответ: d = 0,56 м
3.
Дано:
l = 2 м
R = 0,1 Ом
B = 200 мкТл = 2×10⁻⁶ Тл
--------------------------------------
Найти:
Δq - ?
1) Воспользуемся формулой ЭДС самоиндукций и формулой вектора магнитной индукции на нормаль к элементу., именно по таких формул мы получим общую формулу про ЭДС самоиндукций:
ε = |ΔФ/Δt| - ЭДС самоиндукций (1)
ΔФ = BΔS - Вектор магнитной индукции на нормаль к элементу (2), следовательно:
ε = (BΔS/Δt) - ЭДС самоиндукций
2) Но из этой формулы нам не известно площадь контура, но нам известно что сделан квадрат расположенный горизонтально, следовательно мы получим:
ΔS = S₂ - S₁ - Площадь контура
Где S₂ = 0, тогда S₁ = a² = (l/4)² = l²/16, следовательно:
ΔS = 0 - l²/16 = - l²/16
3) Мы получили площадь контура, теперь мы подставим его в общую формулу про ЭДС самоиндукций:
ε = |(B×(- l²/16))/Δt)| - ЭДС самоиндукций
4) Теперь мы пользуемся законом Ома, именно по такой формулы мы получим из общей формулы про ЭДС самоиндукций, в силу тока самоиндукций:
I = ε/R - Закон Ома, следовательно:
I = (B×l²)/16RΔt) - сила тока самоиндукций
5) И еще мы напишем про силу тока, именно по такой формуле мы найдем заряд провода:
I = Δq/Δt - Сила тока ⇒ Δq = I×Δt - заряд, следовательно:
Объяснение:
Дано:
Необходимо найти: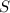 .
.
Как видно из задачи, общий путь между остановками будет равен пути, потраченном на разгон, пути с постоянной скоростью и пути, с постоянным торможением. Разберем каждый участок пути отдельно.
Путь на первом участке, согласно формуле движения с постоянным ускорением будет иметь вид:
Время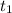 нам известно, неизвестно лишь ускорение
нам известно, неизвестно лишь ускорение  . Так как начальная скорость
. Так как начальная скорость 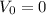 м/с, то можем записать:
м/с, то можем записать:
Ускорение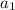 в данном случае будет иметь вид:
в данном случае будет иметь вид: 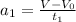 , и если
, и если 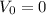 , то получаем:
, то получаем: 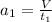
Подставляя в формулу (1) получим:
Можем сразу посчитать:
Вторая часть пути, это путь с постоянной скоростью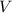 .
.
На данном участке пути, пройденное расстояние будет иметь вид:
Затем, автобус станет тормозить, то есть у нас равнозамедленное движение с постоянным отрицательным ускорением.
Пройденный путь на данном участке будет, согласно формуле равнозамедленного движения:
В данном случае, так как автобус в итоге затормозит и уменьшит свою скорость до нуля (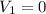 ), то ускорение можно найти согласно формуле:
), то ускорение можно найти согласно формуле:
Если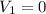 м/с, то ускорение
м/с, то ускорение  будет равно:
будет равно:
Тогда подставляя формулу (3) в формулу (2) получим:
Все данные нам известны, подставляем и считаем:
Теперь, чтобы найти весь путь, пройденный автобусом, сложим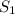 ,
, 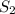 и
и 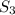 :
:
1.
Дано:
S = 60 см² = 60×10⁻⁴ м²
L = 12 мГн = 0,012 Гн
W₀ = 12 мДж/м³ = 12×10⁻³ Дж/м³
------------------------------------------------
Найти:
1) Для нахождения силы тока в соленоида определяется вот такая формула из энергий магнитного поля, при этой формулы мы найдем силы тока в соленоида:
2) Объемная плотность энергии магнитного поля внутри соленоида определяется по такой формуле именно по такой формуле мы подставим на (1) формулу:
3) Но из формулы (2) нам не известно объем соленоида, но в условий есть длина и площадь, значит мы найдем его, запишем эту формулу и потом мы подставим в формулу (2):
4) Следовательно из формулы (1), (2), (3) мы получим общую формулу для нахождения силы тока в соленоиде:
I = √((2×12×10⁻³ Дж/м³ × 60×10⁻⁴ м² × 0,82 м)/0,012 Гн) = √((24×10⁻³ Дж/м³ × 49,2×10⁻⁴ м³)/0,012 Гн) = √((1180,8×10⁻⁷ Дж)/0,012 Гн) = √(98400×10⁻⁷ А²) = √((98400/10⁷) А²) = (√98400)/(√10⁷) А = (20√(246))/(1000√(10)) А × (√10)/(√10) = (20√(2460))/(1000×10) А = (20√(2460))/10000 А ≈ 0,002×49,5984 А ≈ 0,0991968 А ≈ 0,1 А
ответ: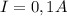
2.
Дано:
Г = 2,5
D = 2,5 Дптр
-----------------------
Найти:
d - ?
Мы находим формулы линзы, именно по такой формуле мы найдем расстояние от линзы до предмета:
Г = f/d - Увеличение линзы
D = 1/F - Оптическая сила линзы
1/F = 1/f + 1/d - Формула линзы, следовательно:
D = 1/f + 1/d ⇒ D = (1/(Г×d)) + 1/d ⇒ D = (1/(Г×d)) + (Г/(Г×d)) ⇒ D = (1+Г)/(Г×d) | × (Г×d) ⇒ D×(Г×d) = 1+Г | : d ⇒ d = (1+Г)/(D×Г) - расстояние от линзы до предмета (4)
d = (1+2,5)/(2,5 Дптр × 2,5) = 3,5/(6,25 Дптр) = 0,56 м
ответ: d = 0,56 м
3.
Дано:
l = 2 м
R = 0,1 Ом
B = 200 мкТл = 2×10⁻⁶ Тл
--------------------------------------
Найти:
Δq - ?
1) Воспользуемся формулой ЭДС самоиндукций и формулой вектора магнитной индукции на нормаль к элементу., именно по таких формул мы получим общую формулу про ЭДС самоиндукций:
ε = |ΔФ/Δt| - ЭДС самоиндукций (1)
ΔФ = BΔS - Вектор магнитной индукции на нормаль к элементу (2), следовательно:
ε = (BΔS/Δt) - ЭДС самоиндукций
2) Но из этой формулы нам не известно площадь контура, но нам известно что сделан квадрат расположенный горизонтально, следовательно мы получим:
ΔS = S₂ - S₁ - Площадь контура
Где S₂ = 0, тогда S₁ = a² = (l/4)² = l²/16, следовательно:
ΔS = 0 - l²/16 = - l²/16
3) Мы получили площадь контура, теперь мы подставим его в общую формулу про ЭДС самоиндукций:
ε = |(B×(- l²/16))/Δt)| - ЭДС самоиндукций
4) Теперь мы пользуемся законом Ома, именно по такой формулы мы получим из общей формулы про ЭДС самоиндукций, в силу тока самоиндукций:
I = ε/R - Закон Ома, следовательно:
I = (B×l²)/16RΔt) - сила тока самоиндукций
5) И еще мы напишем про силу тока, именно по такой формуле мы найдем заряд провода:
I = Δq/Δt - Сила тока ⇒ Δq = I×Δt - заряд, следовательно:
Δq = (B×(-l²))/16RΔt) × Δt = (B×l²))/16R ⇒ Δq = (B×l²)/16R - Заряд провода
Δq = (2×10⁻⁶ Тл)×(2 м)²/16×0,1 Ом = 2×10⁻⁶ (Н/A×м)×4м²/1,6 Ом = 8×10⁻⁶ Н×м/А / 1,6 Ом = 5×10⁻⁶ Кл = 5 мкКл
ответ: Δq = 5 мкКл