Решение. Для каждого вещества существует максимальная длина световой волны (красная граница фотоэффекта), при которой начинается фотоэффект. Облучение вещества световыми волнами, которые имеют большую длину, фотоэффекта не вызывают. Максимальная длина световой волны (минимальная частота) соответствует минимальной энергии фотона: если , то электроны не будут вылетать из вещества. Условие
Дано:Решениеm1 = 0,4 кгm2 = 0,6 кгg = 10м/с2Инерциальную систему отсчета свяжем с Землей. Тело массой m1 взаимодействует с Землей и с нитью, на него действуют сила тяжести Fтяж1 и сила натяжения нитиT1.Тело массой m2 также взаимодействует с Землей инитью. На него действуют сила тяжестиa ?T ? Fтяж 2 и сила натяжения нити T2. Если систему грузов предоставить самой себе, то груз массой m1станет двигаться вверх, а груз массой m2 — вниз.Для каждого тела в соответствии со вторым законом Ньютона запишем уравнение в векторной форме:Fтяж 1 + T1 = m1a1; Fтяж 2 + T2 = m2a2.В проекциях на ось Y (рис. 57) эти уравнения можно записать:Fтяж 1 + T1 = –m1a1; Fтяж 2 + T2 = m2a2.Поскольку массой нити и блока можно пренебречь, то модули сил натяжения T1 и T2 равны, т. е. T1 = T2= T. Так как нить нерастяжима, то ускорения грузов по модулю одинаковы a1 = a2 = a.Получим:m1g – T = –m1a; m2g – T = m2a.Сложим записанные уравнения, умножив первое на (–1):m2g – m1g = m1a + m2a.Откудаa = = .Выразим силу натяжения нити T из первого уравнения:T = m1g + m1a.Подставив выражение для ускорения, получим:T = .a = = 2 м/с2;T = = 4,8 Н.ответ: a = 2 м/с2; T = 4,8 Н.
Дано:
Найти: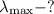
Решение. Для каждого вещества существует максимальная длина световой волны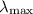 (красная граница фотоэффекта), при которой начинается фотоэффект. Облучение вещества световыми волнами, которые имеют большую длину, фотоэффекта не вызывают. Максимальная длина световой волны (минимальная частота) соответствует минимальной энергии фотона: если
(красная граница фотоэффекта), при которой начинается фотоэффект. Облучение вещества световыми волнами, которые имеют большую длину, фотоэффекта не вызывают. Максимальная длина световой волны (минимальная частота) соответствует минимальной энергии фотона: если 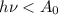 , то электроны не будут вылетать из вещества. Условие
, то электроны не будут вылетать из вещества. Условие
определяет красную границу фотоэффекта.
Таким образом,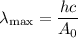
Определим значение искомой величины:
ответ: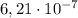 м
м
Fтяж 2 + T2 = m2a2.В проекциях на ось Y (рис. 57) эти уравнения можно записать:Fтяж 1 + T1 = –m1a1;
Fтяж 2 + T2 = m2a2.Поскольку массой нити и блока можно пренебречь, то модули сил натяжения T1 и T2 равны, т. е. T1 = T2= T. Так как нить нерастяжима, то ускорения грузов по модулю одинаковы a1 = a2 = a.Получим:m1g – T = –m1a;
m2g – T = m2a.Сложим записанные уравнения, умножив первое на (–1):m2g – m1g = m1a + m2a.Откудаa = = .Выразим силу натяжения нити T из первого уравнения:T = m1g + m1a.Подставив выражение для ускорения, получим:T = .a = = 2 м/с2;T = = 4,8 Н.ответ: a = 2 м/с2; T = 4,8 Н.