Однородная доска массы 60 кг лежит на двух опорах, как показано на рисунке. Определить силы, действующие на опоры с объяснением

Первая задача:

По закону сохранения энергия:

m * v^2 / 2 = m * g * h, отсюда:

v = (2 * h * g)^0,5 = (2 * 5 * 10)^0,5 = 100^0,5 = 10 метров в секунду.

Ответ: скорость шарика при вылете из пистолета была 10 м/с.

Вторая задача:

Все время падения тела будет равно:

t = (2 * H / g)^0,5 = (2 * 80 / 10)^0,5 = (160 / 10)^0,5 = 16^0,5 равно 4 секунды.

За 3 секунды движения тело пройдет путь:

S1 = g * t^2 / 2 = 10 * 3^2 / 2 = 10 * 9 / 2 = 5 * 9 = 45 метров.

Получается, за последнюю секунду движения тело пройдет путь:

S = H - S1 = 80 - 45 = 35 метров.

Ответ: за последнюю секунду тело пройдет путь, равный 35 метров.

В этой задаче нам закон Снеллиуса (закон преломления света). Угол падения света на поверхность связан с углом преломления соотношением:

, где:

— показатель преломления среды, из которой свет падает на границу раздела;

sinα — угол падения света — угол между падающим на поверхность лучом и нормалью (перпендикуляром) к поверхности;

— показатель преломления среды, в которую свет попадает, пройдя границу раздела;

sinβ— угол преломления света — угол между через поверхность лучом и нормалью к поверхности.

Чтобы начертить дальнейший ход луча, нужно узнать sinβ. Выразим sinβ:

= . В данной задаче n1 = 1 (для воздуха), n2 = 1,333 (для воды).

Вычислим дальнейший ход луча сначала для угла падения 60°:

sinβ =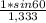 = = 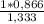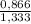≈ 0,6496624

Данному синусу соответствует угол в 40°. Теперь с транспортира строим угол преломления в 40°

Теперь вычислим дальнейший ход луча для угла падения в 30°:

= = ≈ 0,375

Данному синусу соответствует угол в 22°. Опять же с транспортира строим угол преломления.