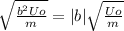При малых отклонениях х функция cos(bx) принимает следующий вид (разложение в ряд Маклорена вблизи нуля): cos(bx) ≈ 1 - = 1 -
⇒ потенциальная энергия будет выглядеть как:
U = U₀·(1 – cos(bx)) ≈ U₀·( 1 - 1 + ) = U₀·, а кинетическая энергия:
Е = , где v = dx/dt = x' – скорость данной частицы. Далее согласно закону сохранения энергии для консервативных систем: Е + U = const, то есть сумма кинетической и потенциальной энергии неизменна во времени. Затем продифференцируем выражение Е + U = const по t:
При малых отклонениях х функция cos(bx) принимает следующий вид (разложение в ряд Маклорена вблизи нуля): cos(bx) ≈ 1 -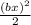 = 1 -
= 1 - 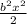
⇒ потенциальная энергия будет выглядеть как:
U = U₀·(1 – cos(bx)) ≈ U₀·( 1 - 1 +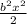 ) = U₀·
) = U₀·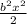 , а кинетическая энергия:
, а кинетическая энергия:
Е =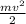 , где v = dx/dt = x' – скорость данной частицы. Далее согласно закону сохранения энергии для консервативных систем: Е + U = const, то есть сумма кинетической и потенциальной энергии неизменна во времени. Затем продифференцируем выражение Е + U = const по t:
, где v = dx/dt = x' – скорость данной частицы. Далее согласно закону сохранения энергии для консервативных систем: Е + U = const, то есть сумма кинетической и потенциальной энергии неизменна во времени. Затем продифференцируем выражение Е + U = const по t:
⇒ U₀·b²x·x' + mx'·x'' = 0 ⇒ x'·(U₀·b²x + m·x'') = 0 ⇒ U₀·b²·x + m·x'' = 0 ⇒
x'' +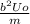 ·x = 0 ⇔ x'' + ω²₀·x = 0 – получилось уравнение гармонических колебаний, где ω₀ - частота малых (собственных) колебаний ⇒
·x = 0 ⇔ x'' + ω²₀·x = 0 – получилось уравнение гармонических колебаний, где ω₀ - частота малых (собственных) колебаний ⇒
ω₀ =