Сразу же оговоримся о том что классическая механика не подразумевает работу с релятивистскими скоростями, а лишь со скоростями многим меньше скорости распространения света в вакууме. - но если в задании просят, то рассчитаем
В классической механике чтобы определить скорость сближения, в нашем случае, мы бы должны были просто сложить эти скорости
Таким образом у нас получилось скорость порядка м/с
Как видно мы получили скорость сближения ракет больше чем скорость распространения света в вакууме, а значит работать с релятивистскими скоростями в классической механике дело в корне неверное
2) в специальной теории относительности
А как раз в СТО работать с релятивистскими скоростями можно и нужно
Тут скорость сближения ракет будет вычисляется следующим образом
Таким образом у нас получилось скорость порядка м/с, что уже не противоречит постулатам СТО
Известно, что потенциальная энергия тела (заряда) может изменяться за счет работы по перемещению тела, совершаемой консервативной силой, действующей со стороны полям:
dA dWp
.
В электростатическом поле на заряд q со стороны поля действует
сила Кулона
F qE
. Тогда работа dA, совершаемая электрическим полем
E
, равна работе силы Кулона при малом перемещении
dl
в пространстве заряда q (рис. 3)
dA (F dl ) q(E dl ) q(E dx E dy E dz)
x y z
.
Работа dA, совершаемая потенциальным полем, приводит к изменению потенциальной энергии dWp заряженного тела
dz
z
dy
y
dx
x
dA dWp qd q .
Из сопоставления этих выражений для работы dA видно, что связь
между напряженностью и потенциалом электростатического поля имеет
вид
x
Ex
,
y
Ey
,
z
Ez
или
E grad
.
Градиент (grad) скалярной
функции – это вектор, направленный в
сторону наиболее быстрого возрастания функции, равный по модулю производной от функции по этому
направлению. Следовательно, напряженность электрического поля
направлена в сторону наиболее
быстрого убывания потенциала.
Единицы измерения потенциала: В (вольт).
Из выражения
dA q(E dl )
следует, что работа по перемещению
заряда вдоль линии напряженности электрического поля
E dl
||
максимальна
dA q E dl . А работа по перемещению заряда перпендикулярно
Объяснение:
--------------------------
1) в классической механике
Сразу же оговоримся о том что классическая механика не подразумевает работу с релятивистскими скоростями, а лишь со скоростями многим меньше скорости распространения света в вакууме. - но если в задании просят, то рассчитаем
В классической механике чтобы определить скорость сближения, в нашем случае, мы бы должны были просто сложить эти скорости
Таким образом у нас получилось скорость порядка
м/с
Как видно мы получили скорость сближения ракет больше чем скорость распространения света в вакууме, а значит работать с релятивистскими скоростями в классической механике дело в корне неверное
2) в специальной теории относительности
А как раз в СТО работать с релятивистскими скоростями можно и нужно
Тут скорость сближения ракет будет вычисляется следующим образом
Таким образом у нас получилось скорость порядка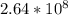
м/с, что уже не противоречит постулатам СТО
Известно, что потенциальная энергия тела (заряда) может изменяться за счет работы по перемещению тела, совершаемой консервативной силой, действующей со стороны полям:
dA dWp
.
В электростатическом поле на заряд q со стороны поля действует
сила Кулона
F qE
. Тогда работа dA, совершаемая электрическим полем
E
, равна работе силы Кулона при малом перемещении
dl
в пространстве заряда q (рис. 3)
dA (F dl ) q(E dl ) q(E dx E dy E dz)
x y z
.
Работа dA, совершаемая потенциальным полем, приводит к изменению потенциальной энергии dWp заряженного тела
dz
z
dy
y
dx
x
dA dWp qd q .
Из сопоставления этих выражений для работы dA видно, что связь
между напряженностью и потенциалом электростатического поля имеет
вид
x
Ex
,
y
Ey
,
z
Ez
или
E grad
.
Градиент (grad) скалярной
функции – это вектор, направленный в
сторону наиболее быстрого возрастания функции, равный по модулю производной от функции по этому
направлению. Следовательно, напряженность электрического поля
направлена в сторону наиболее
быстрого убывания потенциала.
Единицы измерения потенциала: В (вольт).
Из выражения
dA q(E dl )
следует, что работа по перемещению
заряда вдоль линии напряженности электрического поля
E dl
||
максимальна
dA q E dl . А работа по перемещению заряда перпендикулярно
напряженности электрического поля
E dl
минимальна
dA 0.
Интегрируя выражение
dA q(E dl ) qd