Планета имеет массу в 4 раза меньшую массы Земли. Найдите радиус этой планеты, если известно, что ускорение свободного падения на поверхности этой планеты такое же, как на Земле, радиус Земли 6,4 · 106 м. ответ выразите в (км).
За законом Всесвітнього тяжіння, g=GM/. Тоді нехай Rз-радіус Землі, Rп- радіус планети, Mз/Mп=4. Оскільки прискорення вільного падіння на Землі і на планеті однакові, то прирівняємо праві частини рівняння. GMз/Rз^2=GMп/Rп^2, Rп=Rз* (Mп/Мз)^0.5=Rз/2=6400 км/2=3200 км
Відповідь:
3200 км
Пояснення:
За законом Всесвітнього тяжіння, g=GM/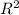 . Тоді нехай Rз-радіус Землі, Rп- радіус планети, Mз/Mп=4. Оскільки прискорення вільного падіння на Землі і на планеті однакові, то прирівняємо праві частини рівняння. GMз/Rз^2=GMп/Rп^2, Rп=Rз* (Mп/Мз)^0.5=Rз/2=6400 км/2=3200 км
. Тоді нехай Rз-радіус Землі, Rп- радіус планети, Mз/Mп=4. Оскільки прискорення вільного падіння на Землі і на планеті однакові, то прирівняємо праві частини рівняння. GMз/Rз^2=GMп/Rп^2, Rп=Rз* (Mп/Мз)^0.5=Rз/2=6400 км/2=3200 км
3200км
Объяснение:
g=γ*M/R^2
На земле g1=γ*M1/R1^2
На планете g2=γ*M2/R2^2
g1=g2
M1=4*M2
R1=6.4*10^6м=6.4*10^3км
γ*M1/R1^2=γ*M2/R2^2
M1/R1^2=M2/R2^2
4*M2/R1^2=M2/R2^2
4/R1^2=1/R2^2
4/(6.4*10^3)^2=1/R2^2
4*R2^2=(6.4*10^3)^2
4*R2^2=40960000
R2^2=10240000=1024*10^4=32^2*10^4
R2 = 3200