Соотношение абсурдное, как и условие. Поясним формулами:
Т = 2Пкор(l/g) - период колебаний математического маятника.
Напишем формулы для ускорения свободного падения для разных высот от центра Земли:
g1 = GM /(R+H)^2
g2 = GM /(R-h)^2
Если период не изменился, значит эти значения g должны быть равны.
Приходим к абсурдному соотношению H = -h.
Делаем вывод, что для обеспечения условия задачи, нужно шахту сделать глубиной больше радиуса Земли, то есть пробуриться глубже центра Земли - к антиподам. Разберем эту ситуацию:
Расстояние до центра Земли от нижней точки шахты: h - R.
Получим следующее уравнение:
R+H = h-R
или: h - H = 2R - судите сами: абсурдно это или нет.
Соотношение абсурдное, как и условие. Поясним формулами:
Т = 2Пкор(l/g) - период колебаний математического маятника.
Напишем формулы для ускорения свободного падения для разных высот от центра Земли:
g1 = GM /(R+H)^2
g2 = GM /(R-h)^2
Если период не изменился, значит эти значения g должны быть равны.
Приходим к абсурдному соотношению H = -h.
Делаем вывод, что для обеспечения условия задачи, нужно шахту сделать глубиной больше радиуса Земли, то есть пробуриться глубже центра Земли - к антиподам. Разберем эту ситуацию:
Расстояние до центра Земли от нижней точки шахты: h - R.
Получим следующее уравнение:
R+H = h-R
или: h - H = 2R - судите сами: абсурдно это или нет.
Если шар полый, то потенциал его внутри постоянен и равен 30 В.
Рассмотрим случай равномерно заряженного по объему целого шара.
Тогда его потенциал на расстоянии r от центра находится по формуле:
ф =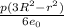 ,
,
где е0 = 8,85*10^(-12) - эл. постоянная, r = 0,05 м, R = 0,1 м, р = q/(4ПR^3/3) - объемная плотность заряда.
Найдем заряд q шара:
Ф = kq/R, где Ф = 30 В, k = 9*10^9
q = ФR/k.
Объемная плотность:
p = 3Ф/(4ПkR^2)
Искомый потенциал шара на расстоянии r от центра:
ф = Ф(3R^2 - r^2) / (2R^2) = 30*(0,03-0,0025)/0,02 = 30(1,5-0,125) =
= 41,25 В.
ответ: 41,25 В ( если шар равномерно заряжен по объему)
Или 30 В (если шар - полый)