На шероховатом участке на брусок будет действовать сила трения, против которой нужно совершить работу. Кинетическая энергия бруска должна быть не меньше этой работы, иначе брусок не преодолеет шероховатый участок.
Значит, m*V0^2/2=Aтр и V0=sqrt(2*Aтр/m)
Известно, что работа механической силы Aтр=Fтр*S.
А вот дальше начинаются проблемы. Где взять массу бруска m, чему равна сила трения Fтр и что за путь S нужно брать в формуле?
Рассмотрим процесс преодоления бруском длинной l шероховатого участка шириной 2l. Здесь можно выделить три участка, для которых рассчитаем Fтр и работу на этом участке
1. Брусок начинает наезжать на шероховатый участок, сила трения пока =0. Постепенно сила трения нарастает до момента, пока брусок полностью не въедет на шероховатую поверхность. Тогда сила трения Fтр= μ*m*g, а путь на этом участке равен длине бруска l. Работу можно вычислить, используя среднее значение силы трения
A1= Fтр.ср*S= Fтр/2* l = μ*m*g /2* l
2. На втором участке брусок целиком находится на шероховатом участке и проходит путь l.
A2= Fтр *S= μ*m*g* l
3. На третьем участке брусок начинает съезжать с шероховатого участка. Сила трения максимальна Fтр= μ*m*g и постепенно снижается до 0 в момент, когда брусок полностью съезжает на гладкую поверхность. Этот случай мы считали на первом участке, только сила изменялась наоборот.
A3= Fтр.ср*S= Fтр/2* l = μ*m*g /2* l
Вся работа против сил трения равна
A=A1+A2+A3=2* μ*m*g* l
Подставляем в формулу для определения скорости. А вот и масса сократилась!
У меня иначе получилось. Фототок насыщения, это явление возникающее при исчерпывании ресурса свободных зарядов. То есть, имея фотоны с энергией выше красной границы, мы можем получать фотоэлектроны в количестве 1 к 1-му, повышая поток фотонов, до тех пор, пока электроны готовые выйти не исчерпаются. Дальнейшее повышение потока фотонов (мощности излучения), не приведёт к росту потока электронов (фототока). И это ключ к пониманию того, что подразумевают авторы под К.П.Д. Они хотят, чтобы мы догадались, что 95% фотонов тратится впустую и только 5% таки выбивают электроны. Остальное просто:
n - число фотонов за время t то есть поток фотонов и он численно равен потоку фотоэлектронов умножая на заряд e обе части, в левой получим ток:
На шероховатом участке на брусок будет действовать сила трения, против которой нужно совершить работу. Кинетическая энергия бруска должна быть не меньше этой работы, иначе брусок не преодолеет шероховатый участок.
Значит, m*V0^2/2=Aтр и V0=sqrt(2*Aтр/m)
Известно, что работа механической силы Aтр=Fтр*S.
А вот дальше начинаются проблемы. Где взять массу бруска m, чему равна сила трения Fтр и что за путь S нужно брать в формуле?
Рассмотрим процесс преодоления бруском длинной l шероховатого участка шириной 2l. Здесь можно выделить три участка, для которых рассчитаем Fтр и работу на этом участке
1. Брусок начинает наезжать на шероховатый участок, сила трения пока =0. Постепенно сила трения нарастает до момента, пока брусок полностью не въедет на шероховатую поверхность. Тогда сила трения Fтр= μ*m*g, а путь на этом участке равен длине бруска l. Работу можно вычислить, используя среднее значение силы трения
A1= Fтр.ср*S= Fтр/2* l = μ*m*g /2* l
2. На втором участке брусок целиком находится на шероховатом участке и проходит путь l.
A2= Fтр *S= μ*m*g* l
3. На третьем участке брусок начинает съезжать с шероховатого участка. Сила трения максимальна Fтр= μ*m*g и постепенно снижается до 0 в момент, когда брусок полностью съезжает на гладкую поверхность. Этот случай мы считали на первом участке, только сила изменялась наоборот.
A3= Fтр.ср*S= Fтр/2* l = μ*m*g /2* l
Вся работа против сил трения равна
A=A1+A2+A3=2* μ*m*g* l
Подставляем в формулу для определения скорости. А вот и масса сократилась!
V0=sqrt(2*Aтр/m)= sqrt(2*2* μ*m*g* l /m)= sqrt(4* μ*g* l)= sqrt(4* 0,1*10* 0,25)=1 м/с
ответ: 1 м/с
У меня иначе получилось. Фототок насыщения, это явление возникающее при исчерпывании ресурса свободных зарядов. То есть, имея фотоны с энергией выше красной границы, мы можем получать фотоэлектроны в количестве 1 к 1-му, повышая поток фотонов, до тех пор, пока электроны готовые выйти не исчерпаются. Дальнейшее повышение потока фотонов (мощности излучения), не приведёт к росту потока электронов (фототока). И это ключ к пониманию того, что подразумевают авторы под К.П.Д. Они хотят, чтобы мы догадались, что 95% фотонов тратится впустую и только 5% таки выбивают электроны. Остальное просто:
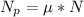
n - число фотонов за время t то есть поток фотонов и он численно равен потоку фотоэлектронов
умножая на заряд e обе части, в левой получим ток:
и переходя к заданным величинам: