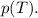Поперечная волна с частотой 30 гц и бежит по натянутому горизонтальную шнуры. расстояние между двумя точками а и б равно 1,5 . определите скорость волны
Закон сложения скоростей, соизмеримых со скоростью света, входит в число основных выводов специальной теории относительности (СТО) , которые приводятся и в школьных учебниках. Вот формула для вычисления: v = (v1 + v2)/ (1 + v1*v2/c (кв) ). Вычислим: учитывая что v1 = v2 = v; : v (отн. ) = (v+ v)/ (1 + v*v./с*с) = 2vс ( кв) /(с (кв) + м (кв) ) = 2*0,8с*с/ (с (кв) + 0,64с (кв) ) = 2*0,8/(1 +0,64) = 1,6/ 1,64 = 0,98 с; Это и можно считать ответом v = 0,98c. Ни при каких скоростях относительная скорость не может превышать скорости света с = 3*10(в 8 ст) м/с. ответ можно выразить и в м/с . v = 0,98*3*10(в 8 ст) м/с = 294 000 000 м/с = 294 000 км/с.
Решение. Применим закон Авогадро: в равных объемах газов при одинаковых температурах и давления содержится одинаковое количество молекул:
где Дж/К — постоянная Больцмана.
Поскольку объем газа не изменяется, то есть имеем изохорный процесс:
Определим количество молекул в начале:
Определим количество молекул в конце:
Тогда число молекул газа изменилось на:
Определим значение искомой величины:
ответ: число молекул увеличилось на
2. Дано:
см² м²
Па
Найти:
Решение. Поскольку бутылку закрыли плотно, то объем газа не изменяется. Значит, имеем изохорный процесс. Изохорный процесс описывается законом Шарля: для данной массы газа отношение давления газа к его температуре является постоянным, если объем газа не меняется:
Сила давления — сила, действующая перпендикулярно к поверхности:
Поскольку сила трения — это внешняя сила, то ее значение равно произведению изменения давления на площадь поперечного сечения пробки:
, откуда
Значит,
Определим значение искомой величины:
ответ: 400 К.
3. Имеем циклический процесс макроскопических параметров. Здесь:
v = (v1 + v2)/ (1 + v1*v2/c (кв) ). Вычислим: учитывая что v1 = v2 = v; : v (отн. ) = (v+ v)/ (1 + v*v./с*с) = 2vс ( кв) /(с (кв) + м (кв) ) = 2*0,8с*с/ (с (кв) + 0,64с (кв) ) = 2*0,8/(1 +0,64) = 1,6/ 1,64 = 0,98 с; Это и можно считать ответом v = 0,98c. Ни при каких скоростях относительная скорость не может превышать скорости света с = 3*10(в 8 ст) м/с. ответ можно выразить и в м/с . v = 0,98*3*10(в 8 ст) м/с = 294 000 000 м/с = 294 000 км/с.
1. Дано:
Найти: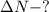
Решение. Применим закон Авогадро: в равных объемах газов при одинаковых температурах и давления содержится одинаковое количество молекул:
где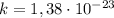 Дж/К — постоянная Больцмана.
Дж/К — постоянная Больцмана.
Поскольку объем газа не изменяется, то есть имеем изохорный процесс: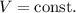
Определим количество молекул в начале:
Определим количество молекул в конце:
Тогда число молекул газа изменилось на:
Определим значение искомой величины:
ответ: число молекул увеличилось на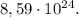
2. Дано:
Найти: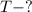
Решение. Поскольку бутылку закрыли плотно, то объем газа не изменяется. Значит, имеем изохорный процесс. Изохорный процесс описывается законом Шарля: для данной массы газа отношение давления газа к его температуре является постоянным, если объем газа не меняется:
Сила давления — сила, действующая перпендикулярно к поверхности:
Поскольку сила трения — это внешняя сила, то ее значение равно произведению изменения давления на площадь поперечного сечения пробки:
Значит,
Определим значение искомой величины:
ответ: 400 К.
3. Имеем циклический процесс макроскопических параметров. Здесь:
Изобразим этот процесс в координатах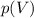 и
и