Построить изображение отрезка ab, расположенного под углом 30° к главной оптической оси и пересекающей её, в собираю щей линзе.

Показать ответ

Ответ:

AliceMysova

01.05.2023 14:10

R = 304 Ом

Объяснение:

Для нахождения сопротивения нам нужно узнать какой ток протекает по проводнику

Для этого воспользуемся формулой Сила Ампера:

$Fa = B \times I \times l \times \sin\alpha$

Из этой формулы сила тока равна:

$I = \frac{Fa}{B \times l \times \sin \alpha }$

Переведём 40 см в м:

40 см = 0,4 м.

Также нам известно что проводник расположен перпендикулярно линиям магнитной индукции. Это значит что:

sin a = 90°

sin90° = 1.

Подставляем значения в формулу и получаем силу тока проходящего по проводик:

$\frac{5}{10 \times0.4 \times 1 } = \frac{5}{4} = 1.25A$

Зная ток можно найти сопротивление по закону Ома для участка цепи:

$I = \frac{ U}{R}$

Отсюда сопротивление равно:

$R = \frac{U }{I}$

Подставляем и решаем:

$\frac{380}{1.25} = 304Ом$

0,0(0 оценок)

Ответ:

Хшж

12.01.2020 07:05

Определим рабочий ток ламы: I=P/U=40/220=0,18 А. Зная напряжение и ток, можно определить сопротивление спирали в рабочем состоянии: R=U/I=220/0,18=1222,22 Ом. Теперь возьмём формулу расчёта сопротивления при изменении температуры: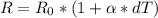 $R=R_{0}*(1+\alpha *dT)$ . Выразим разность температур: 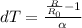$dT=\frac{\frac{R}{R_{0} } -1 }{\alpha }$ . Найдём разность температур: 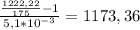$\frac{\frac{1222,22}{175}-1 }{5,1*10^{-3} }=1173,36$ К. Поскольку разница в кельвинах равна разнице в градусах Цельсия, то можно, не переводя одну единицу измерения температуры в другую, сразу прибавить разницу температур к начальной температуре и получить температу спирали в рабочем состоянии: t=20+1173,36=1193,36 °C≈1193 °C.