При делении одного ядра U 92 235 на два осколка выделяется энергия 200 МэВ. Какая энергия освобождается при «сжигании» 6,3 г этого изотопа? Массу одного нуклона считать равной
1,67⋅10−24г.
ответ записать в стандартном виде a⋅10n, где 1
1. (Число a округли до десятых.)
R₂/R₁=√2.
Объяснение:
Запишем для мощности P, Вт на сопротивлении R₁ до замыкания ключа:
P=I²*R₁; I=U/R₁₂;
P=R₁*(U/R₁₂)², где
R₁₂ - эквивалентное сопротивление цепи, Ом до замыкания ключа:
для мощности P', Вт на сопротивлении R₁ после замыкания ключа:
P'=R₁*(U/R₁₂₂)², где
R₁₂₂ - эквивалентное сопротивление цепи, Ом после замыкания ключа:
По условию:
P'/P=2;
P'/P=R₁*(U/R₁₂₂)²/R₁*(U/R₁₂)²=R²₁₂/R²₁₂₂;=2;
R₁₂/R₁₂₂=√2.
Вычислим эквивалентные сопротивления до и после замыкания ключа:
R₁₂=R₁+R₂;
R₁₂₂=R₁+R₂*R₂/(R₂+R₂)=R₁+R₂/2.
Подставим и решаем:
(R₁+R₂)/(R₁+R₂/2)=√2;
R₁+R₂=√2(R₁+R₂/2);
R₁+R₂=√2R₁+√2R₂/2;
R₁+R₂-√2R₁-√2R₂/2=0;
Разделим все на R₁:
R₁/R₁+R₂/R₁-√2R₁/R₁-√2R₂/(2R₁)=0;
1+R₂/R₁-√2-√2R₂/(2R₁)=0;
R₂/R₁(1-√2/2)+1-√2=0;
немного алгебры:
R₂/R₁=(√2-1)/(1-√2/2)=2(√2-1)/(2-√2)=2(√2-1)/(√2(√2-1))=
=2/√2=2√2/2=√2
R₂/R₁=√2.
Проверим. Пусть R₁=1 Ом или относительных единиц, тогда R₂=√2;
R₁₂=1+√2;
R₁₂₂=1+√2/2;
R²₁₂/R²₁₂₂=(1+√2)²/(1+√2/2)²=(1+2√2+2)/(1+√2+1/2)=(3+2√2)/(3/2+√2)=2*(3+2√2)/(3+2√2)=2
Сила тяги: Fт = 650 кН = 6,5 × 10⁵ Н.
Масса: m = 3250 т = 3,25 × 10⁶ Н.
Коэффициент сопротивления: μ = 0,005.
Нужно записать уравнение зависимости скорости от времени.
Решение:1. Уравнение зависимости скорости от времени в общем виде: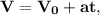 значит, чтобы его записать, нам необходимо знать ускорение и начальную скорость. Про начальную скорость ничего не сказано, принимаем
значит, чтобы его записать, нам необходимо знать ускорение и начальную скорость. Про начальную скорость ничего не сказано, принимаем 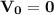 м/с.
м/с.
2. Сделаем рисунок, чтобы лучше понимать задачу (см. приложение). Далее будем расписывать второй закон Ньютона по осям.
3. Запишем силы, действующие на тело по оси Oy: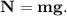
4. Запишем силы, действующие на тело по оси Ox: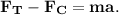
5. Сила сопротивления по определению и с учётом (3):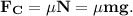
6. Объединяем (4) и (5):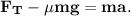
7. Выразим ускорение из (6):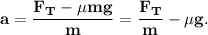
Численно получим:Итак, имеем: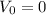 м/с,
м/с, 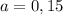 м/с².
м/с².
ответ: