При конденсации пара выделяется количество теплоты Q1=r*m1, где r=2260000 Дж/кг - удельная теплота парообразования воды, m1 - масса пара. Отсюда Q1=2260000*0,06=135600 Дж.
При охлаждении образовавшейся воды от 100С до температуры T выделяется количество теплоты Q2=c1*m1*(100-T), где c1=4200 Дж/(кг*К) - удельная теплоёмкость воды. Отсюда Q2=4200*0,06*(100-T)=252*(100-T)=25200-252*T Дж.
На нагрев льда от -10С до 0С (до температуры плавления) требуется количество теплоты Q3=с2*m2*(0-(-10)), где c2=2100 Дж/(кг*К) - удельная теплоёмкость льда, m2 - его масса. Отсюда Q3=2100*0,4*10=8400 Дж.
На нагрев сосуда от -10С до температуры T требуется количество теплоты Q4=C*(T-(-10)), где C=420 Дж/К - теплоёмкость сосуда. Отсюда Q4=420*(T+10)=420*T+4200 Дж.
На плавление льда требуется количество теплоты Q5=λ*m2, где λ=340000 Дж/кг - удельная теплота плавления льда. Отсюда Q5=340000*0,4=136000 Дж.
На нагрев образовавшейся после таяния льда воды от 0С до температуры T требуется количество теплоты Q6=c1*m2*(T-0). Отсюда Q6=4200*0,4*T=1680*T Дж.
Составляем уравнение теплового баланса: Q1+Q2=Q3+Q4+Q5+Q6. Отсюда следует уравнение 135600+25200-252*T=8400+4200+420*T+136000+1680*T, или 2352*T=12200. Отсюда T=12200/2352≈5,2C. ответ: ≈5,2С.
Запишем уравнение, описывающее количество теплоты, выделящееся в окружающую среду при охлаждении воды массой от до градусов по Цельсию соотвественно:
.
Теперь запишем уравнение, описывающее количество теплоты выделяющееся в окружающую среду при кристаллизации воды массой .
.
Совершенно очевидно, что если полость внутри холодильника (или как там это называется), получит теплоты, то, для сохранения баланса из этой самой полости нужно отвести ровно такое же количество теплоты, поэтому,
Пусть T - искомая температура.
При конденсации пара выделяется количество теплоты Q1=r*m1, где r=2260000 Дж/кг - удельная теплота парообразования воды, m1 - масса пара. Отсюда Q1=2260000*0,06=135600 Дж.
При охлаждении образовавшейся воды от 100С до температуры T выделяется количество теплоты Q2=c1*m1*(100-T), где c1=4200 Дж/(кг*К) - удельная теплоёмкость воды. Отсюда Q2=4200*0,06*(100-T)=252*(100-T)=25200-252*T Дж.
На нагрев льда от -10С до 0С (до температуры плавления) требуется количество теплоты Q3=с2*m2*(0-(-10)), где c2=2100 Дж/(кг*К) - удельная теплоёмкость льда, m2 - его масса. Отсюда Q3=2100*0,4*10=8400 Дж.
На нагрев сосуда от -10С до температуры T требуется количество теплоты Q4=C*(T-(-10)), где C=420 Дж/К - теплоёмкость сосуда. Отсюда Q4=420*(T+10)=420*T+4200 Дж.
На плавление льда требуется количество теплоты Q5=λ*m2, где λ=340000 Дж/кг - удельная теплота плавления льда. Отсюда Q5=340000*0,4=136000 Дж.
На нагрев образовавшейся после таяния льда воды от 0С до температуры T требуется количество теплоты Q6=c1*m2*(T-0). Отсюда Q6=4200*0,4*T=1680*T Дж.
Составляем уравнение теплового баланса: Q1+Q2=Q3+Q4+Q5+Q6. Отсюда следует уравнение 135600+25200-252*T=8400+4200+420*T+136000+1680*T, или 2352*T=12200. Отсюда T=12200/2352≈5,2C. ответ: ≈5,2С.
Запишем уравнение, описывающее количество теплоты, выделящееся в окружающую среду при охлаждении воды массой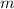
от 
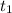до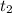 
градусов по Цельсию соотвественно:
Теперь запишем уравнение, описывающее количество теплоты выделяющееся в окружающую среду при кристаллизации воды массой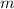
.
Совершенно очевидно, что если полость внутри холодильника (или как там это называется), получит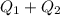
теплоты, то, для сохранения баланса из этой самой полости нужно отвести ровно такое же количество теплоты, поэтому,
Задача в общем виде решена.
Произведем подсчеты.
ответ: 130,5 кДж теплоты.