При проведении лабораторной работы «Определение условия равновесия рычага», к левому плечу рычага были подвешены грузы, общей массой 300г, на расстоянии 4см от оси вращения (рис1.).Определите массу груза, подвешенного к правому плечу рычага. Заполните таблицу опыта.(g≈10 ) Слева от оси Справа от оси
Вес тела в жидкости равен силе тяжести, действующей на тело за вычетом выталкивающей силы. Обозначив за V₁ объем самого метала, а за V₂ внешний объем шарика, можно записать систему уравнений (пренебрегая массой воздуха в полости):
Или, подставив численные значения величин:
Вычитая из первого второе уравнение, найдем внешний объем шарика:
м³
Подставляя результат в первое уравнение, найдем объем метала в шарике:
Не буду рисовать рисунок ! так как у предыдущего ответа есть рисунок я буду по ней решать! треугольник равнобедренный , по свойству касательной проведенной с одной точки ob касательная к окружности, стало быть ве секущая , по формуле ob^2=bk*be =bk(ek+kb) со тоже секущая и она же высота равнобедренного треугольника , по свойству ce*ek=cl*le (точка l это точка где окружность пересекает высоту) у нас известно что ов это середина значит 40/2=20 найдем катет треугольника так как у нас треугольник равнобедренный то 2bc^2=40^2 bc=20√2 теперь найдем высоту треугольника h=√(20√2)^2-20^2 = 20 и найдем отрезок cl=20-2r = 2см ставим все в наше уравнение 400=bk(ek+kb) 40=(ce+ek)*ce се+ek+bk=20√2 решаем систему! сделаем замену чтобы удобней решалось bk=x ek=y ce=z 400=x(y+x) 40=y*(z+y) x+y+z=20√2 выразим y+z третьего уравнения y+z=20√2-x 40=y*(20√2-x) 400=x(y+x) 40=20√2y-yx 400=yx+x^2 40=20√2y-(400-x^2) 440=20√2y+x^2 y=440-x^2/20√2 получаем x =-√82-29√2/2 y=√82 =ek ответ √82
Дано:
____________
Найти: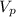
СИ: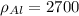 кг/м³;
кг/м³; 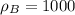 кг/м³;
кг/м³; 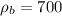 кг/м³;
кг/м³;
Вес тела в жидкости равен силе тяжести, действующей на тело за вычетом выталкивающей силы. Обозначив за V₁ объем самого метала, а за V₂ внешний объем шарика, можно записать систему уравнений (пренебрегая массой воздуха в полости):
Или, подставив численные значения величин:
Вычитая из первого второе уравнение, найдем внешний объем шарика:
Подставляя результат в первое уравнение, найдем объем метала в шарике:
Объем полости:
ответ: 10 см³.