Автомобиль проходит первую треть пути со скоростью v1, а ту часть пути, что осталась, - со скоростью v2 = 50км/час. Определите скорость движения автомобиля (в км/ч) на первом участке пути, если средняя скорость движения автомобиля v(ср.) = 37,5 км/час.
Средняя скорость движения автомобиля равна отношению всего пройденного пути ко всему времени движения: v(cp.) = S/(t₁+t₂)
Обозначим весь путь за единицу. Тогда:
время на прохождение первой трети пути: t₁ = S₁/v₁ = 1/3 : v₁ = 1/3v₁
время на прохождение оставшейся части пути:
t₂ = S₂/v₂ = 2/3 : v₂ = 2/3 : 50 = 1/75
По условию, средняя скорость движения автомобиля равна 37,5 км/ч.
Тогда: 37,5 = 1 : (1/3v₁ + 1/75)
1/3v₁ = 10/375 - 1/75
1/3v₁ = 5/375
15v₁ = 375
v₁ = 25 (км/ч)
ответ: скорость движения автомобиля на первом участке пути 25 км/ч.
Сдвинем всю картинку так, чтобы начальная точка оказалась в начале координат. Это ни на что не влияет. Дальше под координатами я буду понимать сразу сдвинутые координаты.
Известно, что траектория (если не учитывать сопротивление воздуха и прочие прелести реальной жизни) параболическая. Забудем о физике и найдём уравнения траекторий, проходящих через начало координат и заданную точку.
Парабола выпукла вверх, поэтому чтобы вся она была выше какого-то отрезка, достаточно проверить концы этого отрезка. Условие того, что парабола выше какой-то точки:
Подставляем значение b и получается линейное неравенство:
Выписываем такие неравенство для всех точек, решение имеет вид
Подставив t из в , получаем, что
Выражаем компоненты начальной скорости:
Квадрат начальной скорости равен
Его нужно минимизировать. Это можно сделать при производной или численно. Производная даст ответ, что минимальное значение достигается при
Автомобиль проходит первую треть пути со скоростью v1, а ту часть пути, что осталась, - со скоростью v2 = 50км/час. Определите скорость движения автомобиля (в км/ч) на первом участке пути, если средняя скорость движения автомобиля v(ср.) = 37,5 км/час.
Средняя скорость движения автомобиля равна отношению всего пройденного пути ко всему времени движения: v(cp.) = S/(t₁+t₂)
Обозначим весь путь за единицу. Тогда:
время на прохождение первой трети пути: t₁ = S₁/v₁ = 1/3 : v₁ = 1/3v₁
время на прохождение оставшейся части пути:
t₂ = S₂/v₂ = 2/3 : v₂ = 2/3 : 50 = 1/75
По условию, средняя скорость движения автомобиля равна 37,5 км/ч.
Тогда: 37,5 = 1 : (1/3v₁ + 1/75)
1/3v₁ = 10/375 - 1/75
1/3v₁ = 5/375
15v₁ = 375
v₁ = 25 (км/ч)
ответ: скорость движения автомобиля на первом участке пути 25 км/ч.
Сдвинем всю картинку так, чтобы начальная точка оказалась в начале координат. Это ни на что не влияет. Дальше под координатами я буду понимать сразу сдвинутые координаты.
Известно, что траектория (если не учитывать сопротивление воздуха и прочие прелести реальной жизни) параболическая. Забудем о физике и найдём уравнения траекторий, проходящих через начало координат и заданную точку.
Парабола выпукла вверх, поэтому чтобы вся она была выше какого-то отрезка, достаточно проверить концы этого отрезка. Условие того, что парабола выше какой-то точки:
Подставляем значение b и получается линейное неравенство:
Выписываем такие неравенство для всех точек, решение имеет вид
Подставив t из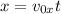 в
в 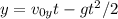 , получаем, что
, получаем, что
Выражаем компоненты начальной скорости:
Квадрат начальной скорости равен
Его нужно минимизировать. Это можно сделать при производной или численно. Производная даст ответ, что минимальное значение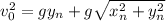 достигается при
достигается при
Если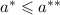 , то ответ - корень из
, то ответ - корень из 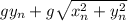 , иначе - корень из
, иначе - корень из