Физика: Принцип руху ракет якшо можна то побистріше

Принцип руху ракет якшо можна то побистріше

Показать ответ

Ответ:

Ирина8891

06.09.2021 06:47

ответ:

объяснение:

\[ t = \frac{m v^{2}}{2} \]

t – кинетическая энергия движущегося тела, m – его масса, v – скорость его движения.

условное обозначение — t

единица измерения энергии — дж (джоуль).

кинетическая энергия характеризует движение тела. это векторная величина. она равна нулю, когда тело неподвижно. кинетическую энергию подразделяют на энергию поступательного и вращательного движения. указанная формула имеет смысл только для поступательного движения.

вот тебе формула извини но я в этом не так силён.

0,0(0 оценок)

Ответ:

rustikkhusnutdi

22.10.2020 03:45

Дано:

q₁ = q₂ = q₃ = q₄ = Q = 10⁻⁷ Кл

Найти: q₀

Изобразим графически все заряды. Заряды в вершинах квадрата пронумеруем от 1 до 4, заряду в центре квадрата присвоим номер 0.

Если система находится в равновесии, то векторная сумма сил, действующих на каждый из зарядов равна 0. Заметим, что поскольку картинка симметрична относительно центрального заряда, то выбирать его для рассмотрения смысла нет. Выберем для рассмотрения один из зарядов, расположенных в вершинах квадрата, например, № 4.

Запишем:

$\vec{F_{41}}+\vec{F_{42}}+\vec{F_{43}}+\vec{F_{40}}=\vec{0}$

Введем ось, на которую спроецируем эти силы. Удобно направить эту ось вдоль диагонали квадрата. Тогда, получим:

$F_{41}\cos\alpha+F_{42}+F_{43}\cos\alpha -F_{40}=0$

$F_{40}=F_{41}\cos\alpha +F_{42}+F_{43}\cos\alpha$

Введенный угол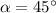 $\alpha =45^\circ$ , так как диагональ квадрата делит его на два равных равнобедренных прямоугольных треугольника.

Подставляя значение косинуса этого угла и расписывая силы Кулона, получим:

$k\dfrac{|q_4||q_0|}{\left(\frac{a\sqrt{2} }{2} \right)^2}=k\dfrac{|q_4||q_1|}{a^2}\cdot\dfrac{\sqrt{2} }{2} +k\dfrac{|q_4||q_2|}{(a\sqrt{2}) ^2}+k\dfrac{|q_4||q_3|}{a^2}\cdot\dfrac{\sqrt{2} }{2}$