Пять лампочек включены в цепь, как показано на рисунке. Сопротивления лампочек указаны на схеме. Найдите отношение Pmax/Pmin, где Pmax — максимальная мощность, выделяющаяся на одной из лампочек цепи, Pmin — минимальная мощность, выделяющаяся на какой-то другой лампочке цепи. ответ округлите до десятых.
Pmax — P (5) = 5 Вт
Pmin — P (2) =2 Вт
Объяснение:
Здесь всё считается по закону Ома: i =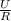
Возьмём для простоты подсчёта сопротивление R = 1 , значит 2R = 2 Ом, 3R = 3 Ом, 4R = 4 Ом, 5R = 5 Ом
Напряжение возьмём U = 9 В (нам ведь не указано конкретное напряжение, мы исследуем цепь).
При последовательном соединении сопротивления суммируются. Давайте их просуммируем (смотрим на схему).
3R означает что он в ТРИ раза больше от R, то есть 3 * R, а R у нас равен R=1, значит 3R = 3 Ом:
3R + 4R = 3 + 4 = 7 Ом
2R + 5R = 2 + 5 = 7 Ом
То есть у нас оказывается 2 цепи с одинаковыми сопротивлениями, в семь раз больше чем у R .
Но эти цепи соединены между собой ПАРАЛЛЕЛЬНО. А при параллельном соединении сопротивления суммируются по формуле:
или по другому R =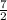
= 3,5 Ом
То есть общее сопротивление из четырёх лампочек R(2,3,4,5,) =3,5 Ом
А ОБЩЕЕ сопротивление во всей цепи равно R(1) + R(2,3,4,5,) = 1 + 3,5 =4,5 Ом
Ток от батарейки в цепи до разветвления везде одинаков: i =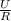
Возьмём напряжение любое, например U = 9 В
Подставляем в формулу тока: i =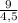
i (1) = 2 А (на первой лампочке)
Напряжение на первой лампочке равно: U(1) = i * R
U(1) = 2 А* 1 Ом = 2 В
Соответственно к остальным лампочкам приложено напряжение:
U(2,3,4,5) = U(общее) - U(1)
U(2,3,4,5) = 9 - 2 = 7 В
Ток в лампочке 2R = 5R i =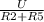
i = 
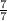= 1 А
Ток в лампочке 3R = 4R i =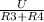
i = 
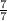= 1 А
Теперь ищем все мощности на лампочках
P = U * i =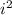
* R
Подставляем и определяем мощности на всех лампочках:
P (1) =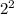
А * 1 Ом = 4 Вт
P (2) =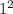
А* 2 Ом =2 Вт
P (3) =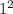
А * 3 Ом=3 Вт
P (4) =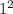
А * 4 Ом=4 Вт
P (5) =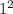
А* 5 Ом=5 Вт
Pmax — P (5) = 5 Вт
Pmin — P (2) =2 Вт