Рівняння швідкості тіла має вигляд : U=4+10t. Запишіть рівняння руху тіла, якщо у момент виключення секундоміра тіло знаходилося на відстані 50 м від початку відліку
Легко! Пусть t = 20000 секунд (я ввел эту величину для удобства). 1) Найдем количество целых часов в t. Для этого поделим t на количество секунд в одном часе (в часе 3600 секунд). Итак,. Отбрасываем дробную часть, она нам не нужна. Для дальнейшей работы нам понадобится остаток от предыдущего деления. Найдем его: . Итак, выходит, что в t ровно 5 целых часов и плюс еще 2000 секунд. 2) Теперь поработаем с этим остатком. Можно найти, сколько минут «вмещается» в 2000 секунд. Для этого поделим эти 2000 секунд на количество секунд в минуте (в минуте 60 секунд). Итак, . Снова отбрасываем дробную часть и снова находим остаток: . Итак, выходит, что в 2000 секунд «вмещается» 33 целых минуты и еще 20 секунд. --------- Так и запишем: t = 5 часов 33 минуты 20 секунд.
км/ч м/с - скорость автобуса на втором участке пути;
с - время, за которое автобус разогнался до скорости, равной 27 км/ч;
с - время движения автобуса с постоянной скоростью, равной 27 км/ч;
с - время торможения автобуса, то есть уменьшения скорости от 27 км/ч до 0.
Необходимо найти: .
Как видно из задачи, общий путь между остановками будет равен пути, потраченном на разгон, пути с постоянной скоростью и пути, с постоянным торможением. Разберем каждый участок пути отдельно.
Путь на первом участке, согласно формуле движения с постоянным ускорением будет иметь вид:
Время нам известно, неизвестно лишь ускорение . Так как начальная скорость м/с, то можем записать:
(1)
Ускорение в данном случае будет иметь вид: , и если , то получаем:
Подставляя в формулу (1) получим:
Можем сразу посчитать:
м. - пройдя расстояние автобус разгонится до скорости 27 км/ч или 7,5 м/с за 5 секунд.
Вторая часть пути, это путь с постоянной скоростью .
На данном участке пути, пройденное расстояние будет иметь вид:
м. - такое расстояние проедет автобус с постоянной скоростью.
Затем, автобус станет тормозить, то есть у нас равнозамедленное движение с постоянным отрицательным ускорением.
Пройденный путь на данном участке будет, согласно формуле равнозамедленного движения:
(2)
В данном случае, так как автобус в итоге затормозит и уменьшит свою скорость до нуля (), то ускорение можно найти согласно формуле:
Если м/с, то ускорение будет равно:
(3)
Тогда подставляя формулу (3) в формулу (2) получим:
Все данные нам известны, подставляем и считаем:
м. - за такое расстояние автобус полностью остановится со скорости м/с за время 8 с.
Теперь, чтобы найти весь путь, пройденный автобусом, сложим , и :
1) Найдем количество целых часов в t. Для этого поделим t на количество секунд в одном часе (в часе 3600 секунд). Итак,
2) Теперь поработаем с этим остатком. Можно найти, сколько минут «вмещается» в 2000 секунд. Для этого поделим эти 2000 секунд на количество секунд в минуте (в минуте 60 секунд). Итак,
---------
Так и запишем:
t = 5 часов 33 минуты 20 секунд.
Объяснение:
Дано:
Необходимо найти: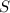 .
.
Как видно из задачи, общий путь между остановками будет равен пути, потраченном на разгон, пути с постоянной скоростью и пути, с постоянным торможением. Разберем каждый участок пути отдельно.
Путь на первом участке, согласно формуле движения с постоянным ускорением будет иметь вид:
Время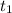 нам известно, неизвестно лишь ускорение
нам известно, неизвестно лишь ускорение  . Так как начальная скорость
. Так как начальная скорость 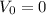 м/с, то можем записать:
м/с, то можем записать:
Ускорение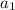 в данном случае будет иметь вид:
в данном случае будет иметь вид: 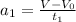 , и если
, и если 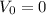 , то получаем:
, то получаем: 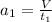
Подставляя в формулу (1) получим:
Можем сразу посчитать:
Вторая часть пути, это путь с постоянной скоростью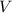 .
.
На данном участке пути, пройденное расстояние будет иметь вид:
Затем, автобус станет тормозить, то есть у нас равнозамедленное движение с постоянным отрицательным ускорением.
Пройденный путь на данном участке будет, согласно формуле равнозамедленного движения:
В данном случае, так как автобус в итоге затормозит и уменьшит свою скорость до нуля (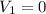 ), то ускорение можно найти согласно формуле:
), то ускорение можно найти согласно формуле:
Если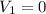 м/с, то ускорение
м/с, то ускорение  будет равно:
будет равно:
Тогда подставляя формулу (3) в формулу (2) получим:
Все данные нам известны, подставляем и считаем:
Теперь, чтобы найти весь путь, пройденный автобусом, сложим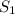 ,
, 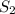 и
и 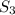 :
: