Рассчитайте массу Юпитера, если известны его радиус~ 7-10'ми ускорение свободного падения на его поверхности 23 м/с Гравитационная постоянная равна 6,7-10-11 Нмё кг).
Пусть - напряжённость электростатического поля создаваемым точечным зарядом . В некоторую точку этого электростатического поля помещают пробный заряд
По определению
Где - сила электростатического взаимодействия между двумя точечными зарядами и
Согласно закону Кулона
Где - расстояние между точечными зарядами и
Преобразуем первую формулу
Как видно из итоговой формулы напряженность электростатического поля создаваемым точечным зарядом никак не зависит от значения модуля пробного заряда внесенного в это поле.
В принципе формулу можно было записать и самого начала и объяснить что так и так. Или даже вовсе не записывать и все объяснить словами.
U^2=P*R, U=√(Р*R).
1) U1=√(1,2*30)=√36=6 (В) - напряжение на R1.
I=U/R - по закону Ома. Отсюда
2) I1=6/30=0,2 (А) - ток через R1.
Т.к. ток в последовательной цепи (из R1 и R2) является constanta, то
3) I2=I1=0,2 (A) - ток через R2.
U=I*R - из закона Ома. Тогда
4) U2=0,2*90=18 (В) - напряжение на R2.
Напряжения в последовательной цепи складываются. Отсюда
5) Uобщ.=U1+U2=6+18=24 (В) - на участке цепи из R1 и R2.
ответ: Общее напряжение на участке цепи 24 В; на участке R1 - 6 В, на участке R2 - 18 В.
ответ: Никак не измениться
Объяснение:
Пусть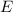 - напряжённость электростатического поля создаваемым точечным зарядом
- напряжённость электростатического поля создаваемым точечным зарядом 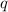 . В некоторую точку этого электростатического поля помещают пробный заряд
. В некоторую точку этого электростатического поля помещают пробный заряд 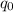
По определению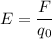
Где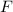 - сила электростатического взаимодействия между двумя точечными зарядами
- сила электростатического взаимодействия между двумя точечными зарядами 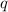 и
и 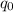
Согласно закону Кулона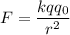
Где - расстояние между точечными зарядами
- расстояние между точечными зарядами 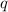 и
и 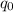
Преобразуем первую формулу
Как видно из итоговой формулы напряженность электростатического поля создаваемым точечным зарядом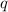 никак не зависит от значения модуля пробного заряда внесенного в это поле.
никак не зависит от значения модуля пробного заряда внесенного в это поле.
В принципе формулу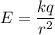 можно было записать и самого начала и объяснить что так и так. Или даже вовсе не записывать и все объяснить словами.
можно было записать и самого начала и объяснить что так и так. Или даже вовсе не записывать и все объяснить словами.