2. При посадке самолёта потенциальная и кинетическая энергия уменьшаются из-за уменьшения высоты и скорости соответственно
3)В процессе падения силами тяжести производится работа, приводящая к переходу потенциальной энергии поднятого молота в кинетическую. При ударе молота о сваю часть кинетической энергии молота переходит во внутреннюю энергию наковальни и молота (и наковальня и молот нагреваются в месте удара). Часть кинетической энергии молота передаётся наковальне - она обретает некоторую скорость. Кинетическая энергия наковальни переходит в тепловую - во внутреннюю энергию молекул наковальни и опоры, на которой она стоит.
Линейной скоростью называется скорость, с которой точка движется по окружности.
Формулу для величины линейной скорости можно вывести на основании следующих рассуждений. Точка, лежащая на окружности радиуса R, за один оборот пройдёт путь, равный длине окружности 2πR, за время, равное периоду Т. Взяв отношение пути 2πR ко времени T, мы получим скорость движения точки по окружности:
2. При посадке самолёта потенциальная и кинетическая энергия уменьшаются из-за уменьшения высоты и скорости соответственно
3)В процессе падения силами тяжести производится работа, приводящая к переходу потенциальной энергии поднятого молота в кинетическую.При ударе молота о сваю часть кинетической энергии молота переходит во внутреннюю энергию наковальни и молота (и наковальня и молот нагреваются в месте удара). Часть кинетической энергии молота передаётся наковальне - она обретает некоторую скорость. Кинетическая энергия наковальни переходит в тепловую - во внутреннюю энергию молекул наковальни и опоры, на которой она стоит.
Линейной скоростью называется скорость, с которой точка движется по окружности.
Формулу для величины линейной скорости можно вывести на основании следующих рассуждений. Точка, лежащая на окружности радиуса R, за один оборот пройдёт путь, равный длине окружности 2πR, за время, равное периоду Т. Взяв отношение пути 2πR ко времени T, мы получим скорость движения точки по окружности:
Так как 1/T = n, где n - число оборотов, то: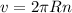
Учитывая ω = 2πn, получим: v = ωR