Осмос наблюдается, когда два раствора различной концентрации (или раствор и чистый растворитель) разделены полупроницаемой перегородкой – мембраной. Полупроницаемой она называется потому, что молекулы растворителя через такую мембрану проходят, тогда, как растворенное соединение ею задерживается. В результате устанавливается направленный поток молекул растворителя из области, где раствор менее концентрированный (молекул растворителя больше), туда, где раствор более концентрированный (там молекул растворителя меньше).После Нолле было проведено много подобных экспериментов. Они интересовали главным образом биологов.Объяснение осмоса.Что происходит при растворении какого-нибудь вещества в растворителе? Молекулы вещества проникают в растворитель, а молекулы растворителя - в область, занятую раствором. Такая взаимная диффузия (проникновение) и приводит к выравниванию концентраций растворённого вещества и растворителя по всему объёму. Теперь представим себе ситуацию, при которой раствор и чистый растворитель разделены полупроницаемой перегородкой - она пропускает молекулы растворителя, но не пропускает молекулы растворённого вещества. Очевидно, что в этом случае выравнивание концентраций может происходить только за счёт односторонней диффузии растворителя. Молекулы растворителя будут перемещаться через мембрану из менее концентрированного раствора в более концентрированный, вызывая в последнем повышение уровня жидкости.
Другими словами можно сказать, что растворитель проникает в раствор под действием сил так называемого осмотического давления. Как только гидростатическое давление столба уравновесит осмотическое давление, процесс прекратится.
Чтобы говорить об осмосе, необходимы три основных условия:
– растворенное в воде вещество
– наличие (или возникновение) полупроницаемой мембраны
– источник воды (растворителя).
Установка для наблюдения явления осмоса
Для демонстрации явления осмоса используется установка, схематически показанная на рис. 2. Главной частью установки является стеклянная колба 1 объемом 0,1 – 0,15 литра, имеющая вид «колокольчика» и закрытая с одной стороны полупроницаемой мембраной 2 из органического целлофана. Края целлофана закрепляются нитками 3 на «юбочке» колокольчика. Колба полностью заполняется подкрашенным раствором сахара 4 (5-10 чайных ложек на литр воды, краситель любой) и плотно закрывается резиновой пробкой 5 нижней, в которую вставлена толстостенная стеклянная трубка длиной 25 – 30 см с внутренним диаметром 1 – 1,5 мм. На трубку надевается небольшое цветное резиновое кольцо 7, показывающее начальный уровень жидкости в трубке. Вторая резиновая пробка 5, надетая на трубку, служит для закрепления всей системы на лабораторном штативе 8. Стеклянная колба с подкрашенным раствором сахара погружается примерно до уровня нижней пробки в стакан с водой 9, стоящий на деревянной подставке 10. Демонстрация явления осмоса на этой установке, при комнатной температуре, будет эффектной, если выполнить ряд условий. Во-первых, в качестве полупроницаемой мембраны хорошо подходит органический целлофан. Такой целлофан при деформации издает характерный хруст, а после смачивания слегка растягивается. Во-вторых, должно быть полностью исключено проникновение раствора в растворитель. Для этого места контакта целлофана и пробки со стеклянной колбой промазывают вазелином или герметиком. Перед закреплением целлофана на колбе он должен быть смочен водой, чтобы находиться в растянутом состоянии. В-третьих, после того как раствор налит в колбу «под горлышко», необходимо выдержать несколько минут для того, чтобы целлофан со стороны раствора успел намокнуть и слегка прогнуться под тяжестью раствора. Этим исключается его дальнейшая деформация и увеличение вследствие этого объема колбы в начале опыта. Начальный уровень раствора в колбе должен быть таким, чтобы после герметизации колбы пробкой уровень раствора в трубке оказался чуть выше пробки. После этого вся система крепится на штативе за верхнюю пробку в вертикальном положении. Расстояние от дна колбы до основания штатива лучше оставить достаточно большим, чтобы можно было снизу подвести стакан с водой, не трогая раннее закрепленную систему. Если утечка раствора незначительна, то на нее можно не обращать внимания, т. к. эксперимент носит характер качественной демонстрации эффекта. Для большей наглядности демонстрации за трубкой помещают белый матовый экран и подсвечивают трубку.
Полупроницаемая мембрана
Полупроницаемой мембраной называется плёнка, пропускающая молекулы растворителя и не пропускающая молекулы растворённого вещества. Пфеффер смачивал сосуды водой, наполнял их растворами гексацианоферрата (III) калия (красной кровяной соли) K3Fe(CN)6 и погружал в раствор медного купороса. При этом в порах сосуда образовывались полупроницаемые мембраны из гексацианоферрата меди Cu3[K3Fe(CN)6]2.
1. В каких направлениях совершаются колебания в продольной волне?
b. Только по направлению распространения волны;
2. От чего зависит громкость звука?
b. От амплитуды колебаний;
3. Динамик подключен к выходу звукового генератора электрических колебаний. Частота колебаний 170 Гц. Определите длину звуковой волны, зная, что скорость звуковой волны в воздухе 340 м/с?
c. 2 м;
4. Как зависит амплитуда вынужденных колебаний от частоты при постоянной амплитуде колебаний вынуждающей силы?
d. Сначала возникает, достигает максимума, а потом убывает. – максимальное значение будет в резонансе, когда частота вынуждающей силы совпадет с резонансной частотой
5. Камертон, прикрепленный к резонансному ящику, ударили резиновым молоточком. К камертону поднесли по очереди два других камертона. Второй камертон в точности такой же, как и первый. Третий – настроен на меньшую частоту. Какой из камертонов начнет звучать с большей амплитудой.
a. Второй – его резонансная частота такая же, как и у первого камертона, поэтому колебания будут с большей амплитудой
Вариант 2.
1. В каких направлениях совершаются колебания в поперечной волне?
c. Только перпендикулярно распространению волны;
2. Чем определяется высота звука?
a. Частотой колебаний;
3. Динамик подключен к выходу звукового генератора электрических колебаний. Частота колебаний 680 Гц. Определите длину звуковой волны, зная, что скорость звуковой волны в воздухе 340 м/с?
a. 0,5 м;
4. Как зависит амплитуда вынужденных колебаний от частоты при постоянной амплитуде колебаний вынуждающей силы?
d. Сначала возникает, достигает максимума, а потом убывает.
5. Камертон, прикрепленный к резонансному ящику, ударили резиновым молоточком. К камертону поднесли по очереди два других камертона. Второй камертон в точности такой же, как и первый. Третий – настроен на большую частоту. Какой из камертонов начнет звучать с большей амплитудой.
a. Второй;
Вариант 3.
1. Графиком механических волн является:
d. Синусоида.
2. В каких упругих средах могут возникать поперечные волны?
c. В твердых телах. – в газах и жидкостях при сдвиге слоя относительно другого нет возвращающей силы
3. От каких физических величин зависит скорость распространения волны:
a. От длины волны;
b. От частоты колебаний волны;
c. От среды, в которой распространяется волна, и ее состояния.
Глупый вопрос. Хотя скорость звука обычно не зависит от длины волны (и, соответственно, частоты), иногда она может зависеть от неё (такое явление называется дисперсией). Дисперсия оптических волн - вообще часто встречающаяся вещь. От среды скорость тоже зависит.
4. В каких упругих средах могут возникать продольные волны:
c. В твердых, жидких и газообразных.
5. Расстояние между ближайшими гребнями волн равно 6 м. Скорость распространения волны 2 м/с. Какова частота ударов волн о берег?
Осмос наблюдается, когда два раствора различной концентрации (или раствор и чистый растворитель) разделены полупроницаемой перегородкой – мембраной. Полупроницаемой она называется потому, что молекулы растворителя через такую мембрану проходят, тогда, как растворенное соединение ею задерживается. В результате устанавливается направленный поток молекул растворителя из области, где раствор менее концентрированный (молекул растворителя больше), туда, где раствор более концентрированный (там молекул растворителя меньше).После Нолле было проведено много подобных экспериментов. Они интересовали главным образом биологов.Объяснение осмоса.Что происходит при растворении какого-нибудь вещества в растворителе? Молекулы вещества проникают в растворитель, а молекулы растворителя - в область, занятую раствором. Такая взаимная диффузия (проникновение) и приводит к выравниванию концентраций растворённого вещества и растворителя по всему объёму. Теперь представим себе ситуацию, при которой раствор и чистый растворитель разделены полупроницаемой перегородкой - она пропускает молекулы растворителя, но не пропускает молекулы растворённого вещества. Очевидно, что в этом случае выравнивание концентраций может происходить только за счёт односторонней диффузии растворителя. Молекулы растворителя будут перемещаться через мембрану из менее концентрированного раствора в более концентрированный, вызывая в последнем повышение уровня жидкости.
Другими словами можно сказать, что растворитель проникает в раствор под действием сил так называемого осмотического давления. Как только гидростатическое давление столба уравновесит осмотическое давление, процесс прекратится.
Чтобы говорить об осмосе, необходимы три основных условия:
– растворенное в воде вещество
– наличие (или возникновение) полупроницаемой мембраны
– источник воды (растворителя).
Установка для наблюдения явления осмоса
Для демонстрации явления осмоса используется установка, схематически показанная на рис. 2. Главной частью установки является стеклянная колба 1 объемом 0,1 – 0,15 литра, имеющая вид «колокольчика» и закрытая с одной стороны полупроницаемой мембраной 2 из органического целлофана. Края целлофана закрепляются нитками 3 на «юбочке» колокольчика. Колба полностью заполняется подкрашенным раствором сахара 4 (5-10 чайных ложек на литр воды, краситель любой) и плотно закрывается резиновой пробкой 5 нижней, в которую вставлена толстостенная стеклянная трубка длиной 25 – 30 см с внутренним диаметром 1 – 1,5 мм. На трубку надевается небольшое цветное резиновое кольцо 7, показывающее начальный уровень жидкости в трубке. Вторая резиновая пробка 5, надетая на трубку, служит для закрепления всей системы на лабораторном штативе 8. Стеклянная колба с подкрашенным раствором сахара погружается примерно до уровня нижней пробки в стакан с водой 9, стоящий на деревянной подставке 10. Демонстрация явления осмоса на этой установке, при комнатной температуре, будет эффектной, если выполнить ряд условий. Во-первых, в качестве полупроницаемой мембраны хорошо подходит органический целлофан. Такой целлофан при деформации издает характерный хруст, а после смачивания слегка растягивается. Во-вторых, должно быть полностью исключено проникновение раствора в растворитель. Для этого места контакта целлофана и пробки со стеклянной колбой промазывают вазелином или герметиком. Перед закреплением целлофана на колбе он должен быть смочен водой, чтобы находиться в растянутом состоянии. В-третьих, после того как раствор налит в колбу «под горлышко», необходимо выдержать несколько минут для того, чтобы целлофан со стороны раствора успел намокнуть и слегка прогнуться под тяжестью раствора. Этим исключается его дальнейшая деформация и увеличение вследствие этого объема колбы в начале опыта. Начальный уровень раствора в колбе должен быть таким, чтобы после герметизации колбы пробкой уровень раствора в трубке оказался чуть выше пробки. После этого вся система крепится на штативе за верхнюю пробку в вертикальном положении. Расстояние от дна колбы до основания штатива лучше оставить достаточно большим, чтобы можно было снизу подвести стакан с водой, не трогая раннее закрепленную систему. Если утечка раствора незначительна, то на нее можно не обращать внимания, т. к. эксперимент носит характер качественной демонстрации эффекта. Для большей наглядности демонстрации за трубкой помещают белый матовый экран и подсвечивают трубку.
Полупроницаемая мембрана
Полупроницаемой мембраной называется плёнка, пропускающая молекулы растворителя и не пропускающая молекулы растворённого вещества. Пфеффер смачивал сосуды водой, наполнял их растворами гексацианоферрата (III) калия (красной кровяной соли) K3Fe(CN)6 и погружал в раствор медного купороса. При этом в порах сосуда образовывались полупроницаемые мембраны из гексацианоферрата меди Cu3[K3Fe(CN)6]2.
1. В каких направлениях совершаются колебания в продольной волне?
b. Только по направлению распространения волны;
2. От чего зависит громкость звука?
b. От амплитуды колебаний;
3. Динамик подключен к выходу звукового генератора электрических колебаний. Частота колебаний 170 Гц. Определите длину звуковой волны, зная, что скорость звуковой волны в воздухе 340 м/с?
c.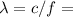
2 м;
4. Как зависит амплитуда вынужденных колебаний от частоты при постоянной амплитуде колебаний вынуждающей силы?
d. Сначала возникает, достигает максимума, а потом убывает. – максимальное значение будет в резонансе, когда частота вынуждающей силы совпадет с резонансной частотой
5. Камертон, прикрепленный к резонансному ящику, ударили резиновым молоточком. К камертону поднесли по очереди два других камертона. Второй камертон в точности такой же, как и первый. Третий – настроен на меньшую частоту. Какой из камертонов начнет звучать с большей амплитудой.
a. Второй – его резонансная частота такая же, как и у первого камертона, поэтому колебания будут с большей амплитудой
Вариант 2.
1. В каких направлениях совершаются колебания в поперечной волне?
c. Только перпендикулярно распространению волны;
2. Чем определяется высота звука?
a. Частотой колебаний;
3. Динамик подключен к выходу звукового генератора электрических колебаний. Частота колебаний 680 Гц. Определите длину звуковой волны, зная, что скорость звуковой волны в воздухе 340 м/с?
a.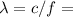
0,5 м;
4. Как зависит амплитуда вынужденных колебаний от частоты при постоянной амплитуде колебаний вынуждающей силы?
d. Сначала возникает, достигает максимума, а потом убывает.
5. Камертон, прикрепленный к резонансному ящику, ударили резиновым молоточком. К камертону поднесли по очереди два других камертона. Второй камертон в точности такой же, как и первый. Третий – настроен на большую частоту. Какой из камертонов начнет звучать с большей амплитудой.
a. Второй;
Вариант 3.
1. Графиком механических волн является:
d. Синусоида.
2. В каких упругих средах могут возникать поперечные волны?
c. В твердых телах. – в газах и жидкостях при сдвиге слоя относительно другого нет возвращающей силы
3. От каких физических величин зависит скорость распространения волны:
a. От длины волны;
b. От частоты колебаний волны;
c. От среды, в которой распространяется волна, и ее состояния.
Глупый вопрос. Хотя скорость звука обычно не зависит от длины волны (и, соответственно, частоты), иногда она может зависеть от неё (такое явление называется дисперсией). Дисперсия оптических волн - вообще часто встречающаяся вещь. От среды скорость тоже зависит.
4. В каких упругих средах могут возникать продольные волны:
c. В твердых, жидких и газообразных.
5. Расстояние между ближайшими гребнями волн равно 6 м. Скорость распространения волны 2 м/с. Какова частота ударов волн о берег?