На высоте h на спутник массы m действует cила тяжести F = γmM/(h+R)², вызывающая ускорение свободного падения a = γM/(h+R)² M - масса Земли γ - гравитационная постоянная R - радиус Земли - 6 400 000 м Чтобы не путаться в порядках большой величины M и малой величины γ предпочитаю где возможно использовать равенство γM = gR² g - ускорение свободного падения близ поверхности Земли Условием движения по круговой орбите радиуса (h + R) c орбитальной скоростью v является равенства упомянутого ускорения a = gR²/(h+R)² центростремительному ускорению a = v²/(h+R) Из уравнения gR²/(h+R)² = a = v²/(h+R) можно получить значение для орбитальной скорости: v² = gR²/(h+R) Для случая h = R это выражение принимает вид: v² = gR²/2R = gR/2 v = √(gR/2) = √(10*6400000/2) = √32000000 = 5660 м в сек (5,66 км в сек)
Отсюда мы видим, что график функции зависимости х от времени-парабола, которая ветвями направлена вниз. Отсюда, график пересекает ось ОХ в двух точках. Но в одной точке значение t будет отрицательное, поэтому этот корень отпадает, потому что время не может быть отрицательным. Теперь находим точку когда х=0:
F = γmM/(h+R)², вызывающая ускорение свободного падения
a = γM/(h+R)²
M - масса Земли
γ - гравитационная постоянная
R - радиус Земли - 6 400 000 м
Чтобы не путаться в порядках большой величины M и малой величины γ предпочитаю где возможно использовать равенство
γM = gR²
g - ускорение свободного падения близ поверхности Земли
Условием движения по круговой орбите радиуса (h + R) c орбитальной скоростью v является равенства упомянутого ускорения
a = gR²/(h+R)²
центростремительному ускорению
a = v²/(h+R)
Из уравнения
gR²/(h+R)² = a = v²/(h+R)
можно получить значение для орбитальной скорости:
v² = gR²/(h+R)
Для случая h = R это выражение принимает вид:
v² = gR²/2R = gR/2
v = √(gR/2) = √(10*6400000/2) = √32000000 = 5660 м в сек (5,66 км в сек)
1) x=-2t^2+4t+5
Отсюда мы видим, что график функции зависимости х от времени-парабола, которая ветвями направлена вниз. Отсюда, график пересекает ось ОХ в двух точках. Но в одной точке значение t будет отрицательное, поэтому этот корень отпадает, потому что время не может быть отрицательным. Теперь находим точку когда х=0:
0=2t^2-4t-5
D=16+40=56
x=0 t=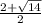
2) Дано- m=0.01кг, h=5м, t=1.2с
Найти - P-?
Решение
h=at^2/2 =>at^2=2h => a=2h/t^2 =>a=10/1.44=6.9 (м/с^2)
строим схему падения тела и получаем уравнение на ось ОУ:
ma=mg-N
N=mg-ma
N=P
P=mg-ma
P=0.01*10-0.01*6.9=0.1-0.069=0.031 (H)
ответ: 0.031 H