Вес тела в жидкости равен силе тяжести, действующей на тело за вычетом выталкивающей силы. Обозначив за V₁ объем самого метала, а за V₂ внешний объем шарика, можно записать систему уравнений (пренебрегая массой воздуха в полости):
Или, подставив численные значения величин:
Вычитая из первого второе уравнение, найдем внешний объем шарика:
м³
Подставляя результат в первое уравнение, найдем объем метала в шарике:
Бочка Паскаля. По указанию Паскаля, крепкую дубовую бочку до краев наполнили водой и наглухо закрыли крышкой. В небольшое отверстие в крышке заделали конец вертикальной стеклянной трубки такой длины, что конец ее оказался на уровне второго этажа. Выйдя на балкон, Паскаль принялся наполнять трубку водой. Не успел он вылить и десятка стаканов, как вдруг, к изумлению обступивших бочку зевак, бочка с треском лопнула. Ее разорвала непонятная сила. Паскаль убеждается: да, сила, разорвавшая бочку, вовсе не зависит от количества воды в трубке. Все дело в высоте, до которой трубка была заполнена. Далее проявляется удивительное свойство воды - передавать давление, создаваемое на ее поверхности (в бочке) по всему объему, каждой точке стенки или дна бочки. Так он приходит к открытию закона, получившего его имя.
Дано:
____________
Найти: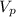
СИ: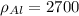 кг/м³;
кг/м³; 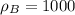 кг/м³;
кг/м³; 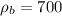 кг/м³;
кг/м³;
Вес тела в жидкости равен силе тяжести, действующей на тело за вычетом выталкивающей силы. Обозначив за V₁ объем самого метала, а за V₂ внешний объем шарика, можно записать систему уравнений (пренебрегая массой воздуха в полости):
Или, подставив численные значения величин:
Вычитая из первого второе уравнение, найдем внешний объем шарика:
Подставляя результат в первое уравнение, найдем объем метала в шарике:
Объем полости:
ответ: 10 см³.
Выйдя на балкон, Паскаль принялся наполнять трубку водой. Не успел он вылить и десятка стаканов, как вдруг, к изумлению обступивших бочку зевак, бочка с треском лопнула. Ее разорвала непонятная сила. Паскаль убеждается: да, сила, разорвавшая бочку, вовсе не зависит от количества воды в трубке. Все дело в высоте, до которой трубка была заполнена.
Далее проявляется удивительное свойство воды - передавать давление, создаваемое на ее поверхности (в бочке) по всему объему, каждой точке стенки или дна бочки.
Так он приходит к открытию закона, получившего его имя.