1.Самоиндукция-явление возникновения эдс. индукции в эл. цепи в результате изменения силы тока. 2.Где L-коэффициент самоиндукции.Из этого выражения определяется единица измерения индуктивностии-Генри. 3.Правило Ленца определяет направление индукционного токав замкнутом контуре при его движении во внешнем магнитном поле. 4.Формула индуктивного сопротивления.При включении катушки индуктивности в цепь переменного тока,под действиемДанная величина связана напрямую с частотой приложенного напряжения и значением индуктивности.
В модели Резерфорда угол рассеяния зависит при прочих постоянных от прицельного параметра (т.е. от расстояния между ядром и первоначальным направлением полета частицы). Зависимость следующая
Проще говоря, если частица врежется прямо в ядро ( b = 0 ), из этой формулы следует что угол рассеяния , т.е. он большой, частица полетит назад.
Ну так вот, как много частиц из потока имеют необходимую величину прицельного параметра? Чтоб можно было полететь назад?
ответ дает формула Резерфорда, утверждающая что
(#)
Поясню обозначения
- число частиц, испытывающих рассеяние в углах от
- общее число частиц в потоке, что летит на металлическую фольгу
А теперь посмотрите на график (#) в прикр. файлах
Видно что относительное число частиц, рассеянных на углах близких к 180 градусам, очень мало. В то же время на небольших углах это число велико. Поэтому в силу этой модели можем утверждать, что лишь малая часть отклониться на большие углы.
2.Где L-коэффициент самоиндукции.Из этого выражения определяется единица измерения индуктивностии-Генри.
3.Правило Ленца определяет направление индукционного токав замкнутом контуре при его движении во внешнем магнитном поле.
4.Формула индуктивного сопротивления.При включении катушки индуктивности в цепь переменного тока,под действиемДанная величина связана напрямую с частотой приложенного напряжения и значением индуктивности.
В модели Резерфорда угол рассеяния зависит при прочих постоянных от прицельного параметра (т.е. от расстояния между ядром и первоначальным направлением полета частицы). Зависимость следующая
Проще говоря, если частица врежется прямо в ядро ( b = 0 ), из этой формулы следует что угол рассеяния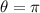 , т.е. он большой, частица полетит назад.
, т.е. он большой, частица полетит назад.
Ну так вот, как много частиц из потока имеют необходимую величину прицельного параметра? Чтоб можно было полететь назад?
ответ дает формула Резерфорда, утверждающая что
Поясню обозначения
А теперь посмотрите на график (#) в прикр. файлах
Видно что относительное число частиц, рассеянных на углах близких к 180 градусам, очень мало. В то же время на небольших углах это число велико. Поэтому в силу этой модели можем утверждать, что лишь малая часть отклониться на большие углы.