рядом находятся 2 противоположно заряженных металлических шарика. первый имеет заряд 0,1 мКл, второй 0,2 мкл.Определите сколько электронов от первого шарика должно перейти на второй чтобы они перестали притягиваться.
Вертикальное положение карандаша в воде - неустойчивое положение и если опустить карандаш вертикально в воду и отпустить, то он займёт горизонтальное положение.. Всё объясняется расположением центра масс.. В кораблестроении есть выражение остойчивость, именно расположение центра масс (метацентра) по отношению к геометрическому центру обуславливает остойчивость (чем ниже центр масс, тем остойчивость выше и тем при больших возмущениях и волнах, стремящихся опрокинуть корабль возвращается обратно).. И карандаш в вертикальном положении уже при малых возмущениях перейдёт в горизонтальное положение.. Сместить его в вертикальное положение просто - сместить центр тяжести грузиком.. И это положение уже будет устойчивым..
1502 м
Объяснение:
Поскольку сопротивлением воздуха можно пренебречь, на тело действует только сила тяжести.
Рассмотрим вертикальный и горизонтальный полет отдельно.
Вертикальное движение мяча является равноускоренным с ускорением g.
Горизонтальное движение является равномерным.
Начальная вертикальная скорость:
Начальная горизонтальная скорость:
Полет заканчивается, когда мяч падает на землю.
Найдем время полета:
Получаем обычное квадратное уравнение. Решая его, при условии что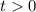 получаем
получаем
За это время горизонтально мяч пролетит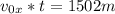
Всё объясняется расположением центра масс..
В кораблестроении есть выражение остойчивость, именно расположение центра масс (метацентра) по отношению к геометрическому центру обуславливает остойчивость (чем ниже центр масс, тем остойчивость выше и тем при больших возмущениях и волнах, стремящихся опрокинуть корабль возвращается обратно)..
И карандаш в вертикальном положении уже при малых возмущениях перейдёт в горизонтальное положение.. Сместить его в вертикальное положение просто - сместить центр тяжести грузиком.. И это положение уже будет устойчивым..