Физика: с физикой - сила после изменения скорости

с физикой - сила после изменения скорости

Показать ответ

Ответ:

Алиса228228

29.07.2022 07:24

Дано:

Объёмы горячей и холодной воды: V₁ = V₂ = V = 3 л = 3 * 10⁻³ м³.

Температура горячей воды (кипения воды): t₁ = 100 °C.

Температура холодной воды: t₂ = 15 °C.

Найти изменение температуры горячей воды Δt₁ - ?Решение:

0. Тепло, полученное от остывания кипятка тратится на нагревание холодной воды. В итоге устанавливается общая температура t.

1. Сразу найдём массу воды: m₁ = m₂ = m = ρV = 1000 * 3 * 10⁻³ = 3 (кг) (на самом деле она нам нужна, почему - узнаете далее).

2. Запишем уравнение теплового баланса: cm(t₁ - t) = cm(t - t₂).

3. Сократим на c и m и (огого!) масса нам больше не нужна: t₁ - t = t - t₂.

4. Выразим общую конечную температуру:

2t = t_1 + t_2;

$t = \frac{t_1 + t_2}{2}.$

5. Тогда изменение температуры горячей воды:

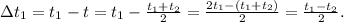
$зt_1 = t_1 - t = t_1 - \frac{t_1 + t_2}{2} = \frac{2t_1 - (t_1 + t_2)}{2} = \frac{t_1 - t_2}{2}.$

Численно получим:

$зt_1 = \frac{100 - 15}{2} = \frac{85}{2} = 42,5$ (°C).

ответ: на 42,5 °C.

0,0(0 оценок)

Ответ:

Ди1218

17.09.2021 12:23

Плотность распределения модулей скоростей
по Максвеллу выражается так:

f(υ) = 4πυ² √[ ( μ/(2πRT) )³ ] exp( -μυ²/(2RT) ) ;

Средняя скорость по Максвеллу:

<υ> = √[ 8RT/(πμ) ] ;

Тогда:

<υ>² = 8RT/(πμ) ;

И:

f(<υ>) = ( 32RT/μ ) √[ ( μ/(2πRT) )³ ] exp( -4/π ) ;

f(<υ>) = ( 16/π ) √[ μ/(2πRT) ] exp( -4/π ) ;

Отсюда доля частиц со скоростями от <υ>–Δυ до <υ>+Δυ,
где Δυ=2<υ>/100, составит:

δ = 2 f(<υ>) <υ>/100 = ( 32/[100π] ) √[ 8RT/(πμ) ] √[ μ/(2πRT) ] exp( -4/π ) =
= ( 0.8/π )² exp( -4/π ) ;

δ = ( 0.8/π )² exp( -4/π ) ≈ 0.018152 ≈ 1.8152 % ; около пары процентов.

0,0(0 оценок)

Популярные вопросы: Физика