С неподвижной лодки массой 40 кг на берег прыгнул мальчик массой 40 кг со скоростью 1м/с, направленной горизонтально. Чему равен модуль скорости лодки относительно берега (ответ в м/с)?

Угол "альфа" - угол между осью оУ и горизонтом. Не забудьте изобразить вектор g, угол "альфа"  - угол между вектором ускорения свободного падения g и осью оХ, изображенной на рисунке в приложении.

Решение подробно изложено в документе Word. 

1. Перемещение будем искать по тоереме Пифагора, зная перемещение в проекции на оси.

2. Запишем в проекции уравнения для нахождения скоростей, затем для перемещений.

3. Путем нехитрых вычислений найдем перемещение тела в проекциях на оси. 

4. Подставим полученные в пп.2-3 значения, в уравнение, записанное в п.1 и, пользуясь основным тригонометрическим тождеством, получаем ответ. 

Подробно в документе Word.

ответ: 125 м

Задача №7

1. Введем прямоуголную систему координат следующим образом, полож. нарпавление оси Оу совпадает с направлением начальной скорости тела, а полож. направление оси Ох совпадает с направлением скорости тела через 5 с, то есть перпендикулярно (по усл.)

2. В векторном виде: S(суммарное)=S(по оси Ох)+S(по оси Оу).

Т.к. угол между векторами 90, то S(суммарное) найдем по теореме Пифагора, зная перемещение вдоль оси Ох, и перемещение вдоль оси Оу.

3. Пусть v0 - начальная скорость, v - скорость тела через время t=5с, y - перемещение тела вдоль оси Оу, х - перемещение тела вдоль оси Ох, угол а - угол между вектором v0 и горизонтом, (а также угол между вектором g и осью Ох), тогда:

Oy:  0=v0-g*sin a*t, где t = 5 c, то есть v0=g*sin a*t

Ox:  v=0+g* cos a*t, то есть v=g*cos a*t

y=v0*t -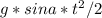 ; так как v0=g*sin a*t, то:

y =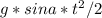 

x=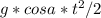

4. s=√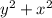

s=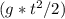√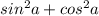, согласно основному тригонометрическому тождеству выражение под корнем равно 1, следовательно корень равен 1, а значит:

s=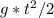

s=10*4*4/2=80(м)

ответ: 80 м