Самолёт держит курс на север со скоростью 300 км/ч относительно воздуха. найдите скорость самолёта относительно земли, если дует западный ветер, скорость которого равна 60 км/ч

Показать ответ

Ответ:

Guttkov

04.09.2022 17:05

Дано:

$\displaystyle \rho_{Al}=2.7$ г/см³;

$\displaystyle \rho_B=1$ г/см³;

$\displaystyle P_B=0.24$ Н;

$\displaystyle \rho_b=0.7$ г/см³;

$\displaystyle P_b=0.33$ Н;

____________

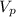
Найти: $\displaystyle V_p$

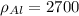СИ: $\displaystyle \rho_{Al}=2700$ кг/м³; $\displaystyle \rho_B=1000$ кг/м³; $\displaystyle \rho_b=700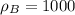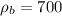$ кг/м³;

Вес тела в жидкости равен силе тяжести, действующей на тело за вычетом выталкивающей силы. Обозначив за V₁ объем самого метала, а за V₂ внешний объем шарика, можно записать систему уравнений (пренебрегая массой воздуха в полости):

$\displaystyle \left \{ {{\rho_{Al}V_1g-\rho_BV_2g=P_B} \atop {\rho_{Al}V_1g-\rho_bV_2g=P_b}} \right.$

Или, подставив численные значения величин:

$\displaystyle \left \{ {{27000V_1-10000V_2=0.24} \atop {27000V_1-7000V_2=0.33}} \right.$

Вычитая из первого второе уравнение, найдем внешний объем шарика:

$\displaystyle -3000V_2=-0.09 = V_2=3*10^{-5}$ м³

Подставляя результат в первое уравнение, найдем объем метала в шарике:

$\displaystyle 27000V_1-0.3=0.24 = V_1=2*10^{-5}$ м³

Объем полости:

$\displaystyle V_p=V_2-V_1=10^{-5}$ м³ или 10 см³

ответ: 10 см³.

0,0(0 оценок)

Ответ:

aram0071

18.01.2023 08:11

1. Твёрдое, жидкое, газообразное

2. В твёрдых - сохраняют объем, то есть не двигаются, в жидких - сохраняют объем, но формы не имеют. Принимают форму сосуда, в котором находятся, обладают таким свойством как текучесть. В газообразных не имеют формы и постоянного объёма, легко сжимаются, молекулы движутся с очень большой скоростью

Объяснение:

3. Количество вещества - физ. величина, характеризуются количество однотипных структурных единиц, содержащихся в веществе.

Формула: v = N/Na, где v это количество вещества, N число частиц вещества и Na это число Авогадро

или v = m/M, где v это количество вещества, m масса вещества и M молярная масса вещества

0,0(0 оценок)

Популярные вопросы: Физика