A) Закон всемирного тяготения, действующий на Земле, будет действовать и на Марсе, и на любой другой планете. Сила тяжести - это частный случай Закона всемирного тяготения:
Fт = m*g
Просто выражаем g из формулы и находим его, подставляя значения из таблицы:
g = F/m = 7,4/2 = 14,8/4 = ... = 3,7 м/с²
Б) В законе всемирного тяготения спрятано g:
Приравняем общий вид Закона к частному случаю, о котором говорили выше:
Тогда выразим квадрат расстояния и найдём само расстояние:
Примерно 3 400 000 м или 3400 км.
В) Найдём через отношение g:
В 4 раза меньше.
Г) Сила тяготения как и любая другая сила, действующая на тело, может являться равнодействующей из Второго закона Ньютона:
Чтобы избежать падения на планету, но быть в достаточно сильном поле её притяжения, необходимо двигаться вокруг планеты, по орбите, с определённой скоростью - первой космической. Движение по орбите - это движение по окружности, где причиной того, что тело двигается криволинейно (по окружности) является центростремительная сила, придающая телу центростремительное ускорение. Этой силой и является сила притяжения:
Или можно записать вот так:
Но мы возьмём первую формулу. Рассчитаем первую космическую у поверхности Марса:
Кинетическая энергия не может быть отрицательной т.к. =m*v^2/2 зависит от массы тела и от скорости тела, масса не может быть отрицательной, а скорость (по формуле) в квадрате, любое число возведённое в квадрат не является отрицательным.
Рассмотрим падение камня со скалы. Предположим что камень стоит на краю скалы (А) скорость камня равна нулю. При падении камня его трение о воздух невелико, поэтому можно считать, что нет перехода энергии в теплоту. Согласно закону сохранения энергии:
Согласно условию задачи в точке А скорость камня равна нулю, поэтому Кинетическая энергия равна нулю. Поскольку указана только одна фиксированная точка – край скалы А, – то разумно принять ее за начало отсчета и сказать что Потенциальная энергия камня равна нулю. Отсюда следует что полная энергия равна нулю:
Следовательно, в силу закона сохранения энергии сумма кинетической и потенциальной энергий камня и Земли остается равной нулю во всех точках траектории:
Сумма двух ненулевых чисел равна нулю только при условии, что одно из них отрицательное, а другое – положительное. Так как кинетическая энергия не может равняться нулю, то потенциальная энергия камня отрицательная. Это связано с выбором нулевого уровня потенциальной энергии. За нулевую точку отсчета координаты h камня мы приняли край скалы. Все точки, через которые пролетает камень, лежат ниже края скалы, и значения координат h этих точек лежат ниже нуля, т.е. они отрицательны.
(как я выше писал кинетическая энергия тела не может быть отрицательной, но в случае котором я привёл или в подобном, где потенциальная энергия - отрицательная, математически можно обе части умножить на минус один тогда: ; )
A) Закон всемирного тяготения, действующий на Земле, будет действовать и на Марсе, и на любой другой планете. Сила тяжести - это частный случай Закона всемирного тяготения:
Fт = m*g
Просто выражаем g из формулы и находим его, подставляя значения из таблицы:
g = F/m = 7,4/2 = 14,8/4 = ... = 3,7 м/с²
Б) В законе всемирного тяготения спрятано g:
Приравняем общий вид Закона к частному случаю, о котором говорили выше:
Тогда выразим квадрат расстояния и найдём само расстояние:
Примерно 3 400 000 м или 3400 км.
В) Найдём через отношение g:
В 4 раза меньше.
Г) Сила тяготения как и любая другая сила, действующая на тело, может являться равнодействующей из Второго закона Ньютона:
Чтобы избежать падения на планету, но быть в достаточно сильном поле её притяжения, необходимо двигаться вокруг планеты, по орбите, с определённой скоростью - первой космической. Движение по орбите - это движение по окружности, где причиной того, что тело двигается криволинейно (по окружности) является центростремительная сила, придающая телу центростремительное ускорение. Этой силой и является сила притяжения:
Или можно записать вот так:
Но мы возьмём первую формулу. Рассчитаем первую космическую у поверхности Марса:
3500 м/с или 3,5 км/с.
Відповідь:
Кинетическая энергия не может быть отрицательной т.к.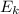
=m*v^2/2 зависит от массы тела и от скорости тела, масса не может быть отрицательной, а скорость (по формуле) в квадрате, любое число возведённое в квадрат не является отрицательным.
Рассмотрим падение камня со скалы. Предположим что камень стоит на краю скалы (А) скорость камня равна нулю. При падении камня его трение о воздух невелико, поэтому можно считать, что нет перехода энергии в теплоту. Согласно закону сохранения энергии:
Согласно условию задачи в точке А скорость камня равна нулю, поэтому Кинетическая энергия равна нулю. Поскольку указана только одна фиксированная точка – край скалы А, – то разумно принять ее за начало отсчета и сказать что Потенциальная энергия камня равна нулю. Отсюда следует что полная энергия равна нулю:
Следовательно, в силу закона сохранения энергии сумма кинетической и потенциальной энергий камня и Земли остается равной нулю во всех точках траектории:
Сумма двух ненулевых чисел равна нулю только при условии, что одно из них отрицательное, а другое – положительное. Так как кинетическая энергия не может равняться нулю, то потенциальная энергия камня отрицательная. Это связано с выбором нулевого уровня потенциальной энергии. За нулевую точку отсчета координаты h камня мы приняли край скалы. Все точки, через которые пролетает камень, лежат ниже края скалы, и значения координат h этих точек лежат ниже нуля, т.е. они отрицательны.
(как я выше писал кинетическая энергия тела не может быть отрицательной, но в случае котором я привёл или в подобном, где потенциальная энергия - отрицательная, математически можно обе части умножить на минус один тогда: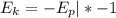
; 
)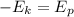