Пусть N N − − мощность отводимого из комнаты тепла с кондиционера. В установившемся режиме ровно столько же тепла проникает через стенки обратно в комнату, поэтому справедлива формула N=α⋅(t у1 −t к1 ), N=α⋅(tу1−tк1), где α α − − некоторая постоянная величина, зависящая от материала и конструкции стенок домика.На следующий день мощность отводимого тепла по условию не изменилась, поэтому верно аналогичное соотношение N=α⋅(t у2 −t к2 ). N=α⋅(tу2−tк2). Приравнивая правые части соотношений для мощности, получаем, что t у1 −t к1 =t у2 −t к2 , tу1−tк1=tу2−tк2, откуда установившаяся на следующий день температура равна t к2 =t у2 −t у1 +t к1 =24 ∘ C. tк2=tу2−tу1+tк1=24∘C.
Сдвинем всю картинку так, чтобы начальная точка оказалась в начале координат. Это ни на что не влияет. Дальше под координатами я буду понимать сразу сдвинутые координаты.
Известно, что траектория (если не учитывать сопротивление воздуха и прочие прелести реальной жизни) параболическая. Забудем о физике и найдём уравнения траекторий, проходящих через начало координат и заданную точку.
Парабола выпукла вверх, поэтому чтобы вся она была выше какого-то отрезка, достаточно проверить концы этого отрезка. Условие того, что парабола выше какой-то точки:
Подставляем значение b и получается линейное неравенство:
Выписываем такие неравенство для всех точек, решение имеет вид
Подставив t из в , получаем, что
Выражаем компоненты начальной скорости:
Квадрат начальной скорости равен
Его нужно минимизировать. Это можно сделать при производной или численно. Производная даст ответ, что минимальное значение достигается при
Сдвинем всю картинку так, чтобы начальная точка оказалась в начале координат. Это ни на что не влияет. Дальше под координатами я буду понимать сразу сдвинутые координаты.
Известно, что траектория (если не учитывать сопротивление воздуха и прочие прелести реальной жизни) параболическая. Забудем о физике и найдём уравнения траекторий, проходящих через начало координат и заданную точку.
Парабола выпукла вверх, поэтому чтобы вся она была выше какого-то отрезка, достаточно проверить концы этого отрезка. Условие того, что парабола выше какой-то точки:
Подставляем значение b и получается линейное неравенство:
Выписываем такие неравенство для всех точек, решение имеет вид
Подставив t из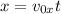
в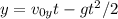 
, получаем, что
Выражаем компоненты начальной скорости:
Квадрат начальной скорости равен
Его нужно минимизировать. Это можно сделать при производной или численно. Производная даст ответ, что минимальное значение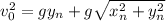
достигается при
Если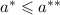
, то ответ - корень из 
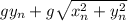, иначе - корень из