Со дна реки глубиной 4 м поднимают камень объемом 0,6 м^3 на баржу,высота борта которой над поверхностью реки 1 м. Плотность камня 1500 кг/м^3. Найдите работу по подъему камня
1. Водитель автомобиля начал торможение, когда находился на расстоянии 200 м от заправочной станции и двигался к ней со скоростью 20 м/с. Какой должна быть сила торможения, чтобы автомобиль массой 1 т остановился около станции?
Дано:
м
м/с
т кг
Найти:
Решение. Направим горизонтальную ось в сторону торможения автомобиля. Перейдем от проекций к модулям:
Тогда откуда
Применим второй закон Ньютона:
Определим значение искомой величины:
ответ: 1 кН
2. Сани движутся по горизонтальной дороге с начальной скоростью 5 м/с, коэффициент трения при этом равен 0,1. Найдите путь, который сани за 3 с.
Дано:
м/с
м/с²
Найти:
Решение. Направим горизонтальную ось в сторону движения саней. Перейдем от проекций к модулям:
Тогда откуда
Найдем
Применим второй закон Ньютона:
Сила трения:
Поскольку , то
Таким образом,
Определим значение искомой величины:
м
ответ: 19,5 м.
3. Автобус массой 10 т, двигаясь с места, развил на пути 50 м скорость 10 м/с. Найдите коэффициент трения, если сила тяги равна 14 кН.
Дано:
т кг
м
м/с
кН
м/с²
Найти:
Решение. Направим горизонтальную ось в сторону движения автобуса. Перейдем от проекций к модулям:
извините если немного не так. или не перевела. я старалась)
Объяснение:
При движении по круговой орбите у спутника есть центростремительное ускорение,
aц=
υ
2
R
. С другой стороны это ускорение вызвано единственной гравитационной силой притяжения к земле и равно ускорению свободного падения g на данной высоте, т.е.: g=
υ
2
R
. Из последней формулы выражаем скорость (которая, кстати, будет равна первой космической скоростью на данной высоте): υ=
g·R
. В данном случае R - радиус круговой орбиты, равный сумме радиуса Земли и высоты над её поверхностью: R= Rз+ h . Ускорение свободного падения тоже зависит от высоты над поверхностью нашей планеты и рассчитывается так: g=
GMз
(Rз+ h)
2
, где G - гравитационная постоянная, а Mз - масса Земли (она не дана в задаче, но её можно найти в справочниках). Подставляя формулы для g и R в формулу для скорости, получаем: υ=
1. Водитель автомобиля начал торможение, когда находился на расстоянии 200 м от заправочной станции и двигался к ней со скоростью 20 м/с. Какой должна быть сила торможения, чтобы автомобиль массой 1 т остановился около станции?
Дано:
Найти: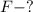
Решение. Направим горизонтальную ось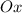 в сторону торможения автомобиля. Перейдем от проекций к модулям:
в сторону торможения автомобиля. Перейдем от проекций к модулям:
Тогда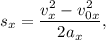 откуда
откуда 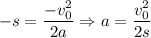
Применим второй закон Ньютона: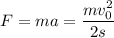
Определим значение искомой величины:
ответ: 1 кН
2. Сани движутся по горизонтальной дороге с начальной скоростью 5 м/с, коэффициент трения при этом равен 0,1. Найдите путь, который сани за 3 с.
Дано:
Найти: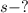
Решение. Направим горизонтальную ось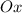 в сторону движения саней. Перейдем от проекций к модулям:
в сторону движения саней. Перейдем от проекций к модулям:
Тогда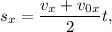 откуда
откуда 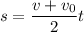
Найдем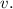
Применим второй закон Ньютона: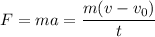
Сила трения: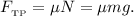
Поскольку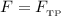 , то
, то
Таким образом,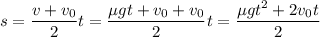
Определим значение искомой величины:
ответ: 19,5 м.
3. Автобус массой 10 т, двигаясь с места, развил на пути 50 м скорость 10 м/с. Найдите коэффициент трения, если сила тяги равна 14 кН.
Дано:
Найти:
Решение. Направим горизонтальную ось в сторону движения автобуса. Перейдем от проекций к модулям:
в сторону движения автобуса. Перейдем от проекций к модулям:
Тогда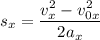 , откуда
, откуда 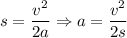
Применим второй закон Ньютона: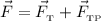
Перейдем от векторов к модулям:
Определим значение искомой величины:
ответ: 0,04.
извините если немного не так. или не перевела. я старалась)
Объяснение:
При движении по круговой орбите у спутника есть центростремительное ускорение,
aц=
υ
2
R
. С другой стороны это ускорение вызвано единственной гравитационной силой притяжения к земле и равно ускорению свободного падения g на данной высоте, т.е.: g=
υ
2
R
. Из последней формулы выражаем скорость (которая, кстати, будет равна первой космической скоростью на данной высоте): υ=
g·R
. В данном случае R - радиус круговой орбиты, равный сумме радиуса Земли и высоты над её поверхностью: R= Rз+ h . Ускорение свободного падения тоже зависит от высоты над поверхностью нашей планеты и рассчитывается так: g=
GMз
(Rз+ h)
2
, где G - гравитационная постоянная, а Mз - масса Земли (она не дана в задаче, но её можно найти в справочниках). Подставляя формулы для g и R в формулу для скорости, получаем: υ=
GMз
Rз+ h
. Теперь расчет: υ=
6,67·10
−11
(Н·м
2
/кг
2
) · 6·10
24
кг
6,4·10
6
м+ 0,6·10
6
м
= 7561,18 м/с