1. Введем прямоуголную систему координат следующим образом, полож. нарпавление оси Оу совпадает с направлением начальной скорости тела, а полож. направление оси Ох совпадает с направлением скорости тела через 5 с, то есть перпендикулярно (по усл.)
2. В векторном виде: S(суммарное)=S(по оси Ох)+S(по оси Оу).
Т.к. угол между векторами 90, то S(суммарное) найдем по теореме Пифагора, зная перемещение вдоль оси Ох, и перемещение вдоль оси Оу.
3. Пусть v0 - начальная скорость, v - скорость тела через время t=5с, y - перемещение тела вдоль оси Оу, х - перемещение тела вдоль оси Ох, угол а - угол между вектором v0 и горизонтом, (а также угол между вектором g и осью Ох), тогда:
Oy: 0=v0-g*sin a*t, где t = 5 c, то есть v0=g*sin a*t
Ox: v=0+g* cos a*t, то есть v=g*cos a*t
y=v0*t - ; так как v0=g*sin a*t, то:
y =
x=
4. s=√
s=√, согласно основному тригонометрическому тождеству выражение под корнем равно 1, следовательно корень равен 1, а значит:
После того как Эрстед обнаружил, что электрические токи создают магнитные поля, было много попыток обнаружить обратный эффект. Может ли сильное магнитное поле вызвать каким-либо образом электрический ток? Исследователи, помещая проводники разной формы и разной природы в магнитные поля, с чувствительных приборов пытались обнаружить слабые токи, которые могли бы при этом возникнуть. Но все попытки заканчивались неудачей. И только в 1831 г. Майклом Фарадеем было сделано одно из наиболее фундаментальных открытий в электродинамике – он доказал явление электромагнитной индукции. Оно заключается в том, что в замкнутом проводящем контуре при изменении магнитного потока, охватываемого этим контуром, возникает электрический ток, который называется индукционным током.

Рассмотрим некоторые опыты, иллюстрирующие явление электромагнитной индукции. Воспользуемся катушкой с большим числом витков, концы которой присоединены к чувствительному гальванометру (рис. 6.1а). При перемещении внутри катушки постоянного магнита стрелка гальванометра отклоняется, то есть в катушке возникает электрический ток (рис. 6.1б). Как только магнит останавливается, ток исчезает (рис. 6.1в). Если магнит движется в обратном направлении, в катушке снова возникает электрический ток, но направление тока будет противоположно первому (рис. 6.1г). Ток возникает и в том случае, когда движется катушка, а магнит находится в покое.
Таким образом, ток возникает только тогда, когда проводники и магнитные поля находятся в относительном движении, причем при сближении катушки и магнита и при удалении их друг от друга возникающие токи имеют противоположные направления. Кроме того, сила индукционного тока тем больше, чем больше скорость относительного движения магнита и катушки. Вместо магнита можно взять другую катушку, соединенную с источником тока. И вновь при вдвигании одной катушки в другую или выдвигании катушки гальванометр будет регистрировать электрический ток. Если катушки неподвижны относительно друг друга, то ток не возникает.
Задача №7
1. Введем прямоуголную систему координат следующим образом, полож. нарпавление оси Оу совпадает с направлением начальной скорости тела, а полож. направление оси Ох совпадает с направлением скорости тела через 5 с, то есть перпендикулярно (по усл.)
2. В векторном виде: S(суммарное)=S(по оси Ох)+S(по оси Оу).
Т.к. угол между векторами 90, то S(суммарное) найдем по теореме Пифагора, зная перемещение вдоль оси Ох, и перемещение вдоль оси Оу.
3. Пусть v0 - начальная скорость, v - скорость тела через время t=5с, y - перемещение тела вдоль оси Оу, х - перемещение тела вдоль оси Ох, угол а - угол между вектором v0 и горизонтом, (а также угол между вектором g и осью Ох), тогда:
Oy: 0=v0-g*sin a*t, где t = 5 c, то есть v0=g*sin a*t
Ox: v=0+g* cos a*t, то есть v=g*cos a*t
y=v0*t -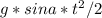
; так как v0=g*sin a*t, то:
y =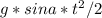
x=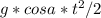
4. s=√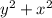
s=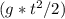
√
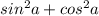, согласно основному тригонометрическому тождеству выражение под корнем равно 1, следовательно корень равен 1, а значит:
s=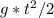
s=10*4*4/2=80(м)
ответ: 80 м
Объяснение:
6. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
6.1. Явление электромагнитной индукции
После того как Эрстед обнаружил, что электрические токи создают магнитные поля, было много попыток обнаружить обратный эффект. Может ли сильное магнитное поле вызвать каким-либо образом электрический ток? Исследователи, помещая проводники разной формы и разной природы в магнитные поля, с чувствительных приборов пытались обнаружить слабые токи, которые могли бы при этом возникнуть. Но все попытки заканчивались неудачей. И только в 1831 г. Майклом Фарадеем было сделано одно из наиболее фундаментальных открытий в электродинамике – он доказал явление электромагнитной индукции. Оно заключается в том, что в замкнутом проводящем контуре при изменении магнитного потока, охватываемого этим контуром, возникает электрический ток, который называется индукционным током.

Рассмотрим некоторые опыты, иллюстрирующие явление электромагнитной индукции. Воспользуемся катушкой с большим числом витков, концы которой присоединены к чувствительному гальванометру (рис. 6.1а). При перемещении внутри катушки постоянного магнита стрелка гальванометра отклоняется, то есть в катушке возникает электрический ток (рис. 6.1б). Как только магнит останавливается, ток исчезает (рис. 6.1в). Если магнит движется в обратном направлении, в катушке снова возникает электрический ток, но направление тока будет противоположно первому (рис. 6.1г). Ток возникает и в том случае, когда движется катушка, а магнит находится в покое.
Таким образом, ток возникает только тогда, когда проводники и магнитные поля находятся в относительном движении, причем при сближении катушки и магнита и при удалении их друг от друга возникающие токи имеют противоположные направления. Кроме того, сила индукционного тока тем больше, чем больше скорость относительного движения магнита и катушки. Вместо магнита можно взять другую катушку, соединенную с источником тока. И вновь при вдвигании одной катушки в другую или выдвигании катушки гальванометр будет регистрировать электрический ток. Если катушки неподвижны относительно друг друга, то ток не возникает.
можно "лучший ответ)"