(1) - это утверждение верно, поскольку графики участков AB и CD являются прямолинейными, а значит скорости на этих участках равны
(2) - это утверждение неверно, поскольку если участок DE действительно соответствует состоянию покоя тела, то вот участок AB соответствует равномерному движению тела.
(3) - это утверждение неверно, поскольку на участке DE тело покоилось
(4) Рассмотрим скорость на участках, где тело двигалось. м/с, м/с, , а значит утверждение верно
(5) это утверждение неверно, поскольку на участках DE и BC тело вообще покоилось
Период вращения — время одного полного оборота. Период вращения {\displaystyle T}T и его частота {\displaystyle \nu }\nu связаны соотношением {\displaystyle T=1/\nu }{\displaystyle T=1/\nu }.
Линейная скорость точки, находящейся на расстоянии {\displaystyle R}R от оси вращения
{\displaystyle v={2\pi \nu R}={2\pi R \over T},}{\displaystyle v={2\pi \nu R}={2\pi R \over T},}
Угловая скорость вращения тела — аксиальный вектор (псевдовектор).
Свойства твердого тела при его вращении описываются моментом инерции твёрдого тела. Эта характеристика входит в дифференциальные уравнения, полученные из уравнений Гамильтона или Лагранжа. Кинетическую энергию вращения можно записать в виде:
В этой формуле момент инерции играет роль массы, а угловая скорость — роль скорости. Момент инерции выражает геометрическое распределение массы в теле и может быть найден из формулы
Момент инерции — физическая величина, мера инертности тела во вращательном движении. Характеризует распределение масс в теле. Различают осевой и центробежный момент инерции. Осевой момент инерции определяется равенством:
(1) - это утверждение верно, поскольку графики участков AB и CD являются прямолинейными, а значит скорости на этих участках равны
(2) - это утверждение неверно, поскольку если участок DE действительно соответствует состоянию покоя тела, то вот участок AB соответствует равномерному движению тела.
(3) - это утверждение неверно, поскольку на участке DE тело покоилось
(4) Рассмотрим скорость на участках, где тело двигалось.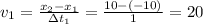
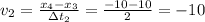м/с, 
м/с,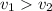 
, а значит утверждение верно
(5) это утверждение неверно, поскольку на участках DE и BC тело вообще покоилось
ответ: 1 и 4Объяснение:
Кинематические характеристики
Вращение характеризуется углом измеряющимся в градусах или радианах, угловой скоростью {\displaystyle \omega ={\frac {d\varphi }{dt}}}\omega ={\frac {d\varphi }{dt}} (измеряется в рад/с) и угловым ускорением {\displaystyle \epsilon ={\frac {d^{2}\varphi }{dt^{2\epsilon ={\frac {d^{{2}}\varphi }{dt^{{2 (единица измерения — рад/с²).
При равномерном вращении ({\displaystyle T}T — период вращения),
Частота вращения — число оборотов в единицу времени.
{\displaystyle \nu ={1 \over T}={\omega \over 2\pi },}{\displaystyle \nu ={1 \over T}={\omega \over 2\pi },}
Период вращения — время одного полного оборота. Период вращения {\displaystyle T}T и его частота {\displaystyle \nu }\nu связаны соотношением {\displaystyle T=1/\nu }{\displaystyle T=1/\nu }.
Линейная скорость точки, находящейся на расстоянии {\displaystyle R}R от оси вращения
{\displaystyle v={2\pi \nu R}={2\pi R \over T},}{\displaystyle v={2\pi \nu R}={2\pi R \over T},}
Угловая скорость вращения тела — аксиальный вектор (псевдовектор).
{\displaystyle \omega ={2\pi \nu }={2\pi \over T}.}{\displaystyle \omega ={2\pi \nu }={2\pi \over T}.}
Динамические характеристики
Свойства твердого тела при его вращении описываются моментом инерции твёрдого тела. Эта характеристика входит в дифференциальные уравнения, полученные из уравнений Гамильтона или Лагранжа. Кинетическую энергию вращения можно записать в виде:
{\displaystyle E={\frac {\omega ^{2}J}{2}}={2\pi ^{2}\nu ^{2}J}.}{\displaystyle E={\frac {\omega ^{2}J}{2}}={2\pi ^{2}\nu ^{2}J}.}
В этой формуле момент инерции играет роль массы, а угловая скорость — роль скорости. Момент инерции выражает геометрическое распределение массы в теле и может быть найден из формулы
{\displaystyle J=\int r^{2}dm.}{\displaystyle J=\int r^{2}dm.}
Момент инерции — физическая величина, мера инертности тела во вращательном движении. Характеризует распределение масс в теле. Различают осевой и центробежный момент инерции. Осевой момент инерции определяется равенством:
{\displaystyle J_{a}=\sum _{i=1}^{n}m_{i}r_{i}^{2},}{\displaystyle J_{a}=\sum _{i=1}^{n}m_{i}r_{i}^{2},}
где {\displaystyle m_{i}}m_i — масса, {\displaystyle r_{i}}r_{i} — расстояние от {\displaystyle i}i-й точки до оси