Среди описанных ситуаций выбери примеры диффузии. Большой резиновый шар, наполненный водородом, через несколько часов сдувается.
На столе вагона поезда лежат фотоаппарат и мяч. Когда поезд тронулся, мяч покатился.
Сплющенный мяч быстро принимает свою прежнюю форму, если на него перестают действовать деформирующие силы.
Дым из трубы дома перестаёт быть видимым через некоторое время (даже в безветренную погоду).
Открытую колбу с углекислым газом уравновесили на весах. Через некоторое время равновесие весов нарушилось.
Для начала нужно нарисовать график S(t), чтобы понять как двигаются автомобили со скоростью v=40 (км/ч), и какие могут быть ещё варианты. По оси S обозначим километраж ( 0, 1000, 2000, 3000 , 4000 и тд (м) ), а по оси t время ( 0, 30, 60, 90 и тд (с) ), к сожалению, фотоаппарата сейчас нет, приходится описывать всё на словах.. Далее нарисовав этот график обозначим красные сигналы светофора. Чтобы автомобиль двигался всё время движения начать он должен с зелённого сигнала. ( Для удобство можно провести на графике линии обозначающие зелёный и красный сигнал светофора ). Тогда получаем что в S=0 от 0 до 30 с сигнал зелённый, далее все промежутки чередуем ( красный-зелёный ). В точке S=1000 от 0 до 30 сек сигнал светофора должен быть красным и тд. Получается такая зависимость. Далее проводим через зелёные участки прямые и получаем, что у нас есть только 3 случая с которыми могут ехать автомобили. Из графика будет видно что автомобили могут иметь такое движение только если будут преодолевать расстояние 1000 м за 30, 90, 150 с. То есть получается зависимость: t=30+60n, где n=0,1,2. Тогда v0=S/t=1/(30+60n)=120/(2n+1). v1=120 ( км/ч ), v2=40 ( км/ч ), v3= 24 ( км/ч ). Для удобства подсчёта v0 перевёл всё в км и ч.
Введем систему координат с началом в точке отправления мяча (см. рисунок).
Запишем законы движения по осям:
(1)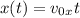
(2)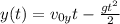
По условию известна скорость в точке 1, где y=h.
Найдем время полета мяча до кольца:
Имеем квадратное уравнение относительно t, его решения:
Скорость мяча найдем, дифференцируя уравнения (1) и (2):
(3)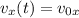
(4)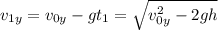 .
.
По теореме Пифагора:
Отсюда, окончательно имеем:
Подставим сюда значения из условия:
v₀ = √(9 + 2*9.8*1) = 5.3 м/с