Стенки вагона поезда , движущегося со скоростью 72км/час , были пробиты пулей , летевшей перпендикулярно к движению вагона. Одно отверстие в стенках вагона смещено относительно другого на s=6см. Ширина вагона d=2,7м. Какова скорость полета пули? Считать ,что стенки вагона настолько тонкие , что траектория движения пули и его скорость не изменилась после того ,как она пробила первую стенку.
ответ: 900 м/с.
Объяснение:
Пусть v=72 км/ч=72/3,6=20 м/с - скорость вагона, d=2,7 м - его ширина, s=6 см=0,06 м - путь, пройденный вагоном за время t полёта пули между его стенками. Тогда t=s/v=0,06/20=0,003 с. Скорость пули v1=d/t=2,7/0,003=900 м/с.
900 м/с
Объяснение:
Дано:
d=2,7 м
U=72 км/ч = 20 м/с (СИ)
l=6 см = 0,06 м (СИ)
Найти:
u-?
Время движения пули, которое мы будем считать равномерным прямолинейным в вагоне(пренебрежём изменение скорости пути во время её взаимодействия со стенками вагона):
u- Скорость движения пути
Время перемещения вагона на расстояние l (Этим обусловлено смещение входного и выходного отверстия пули):
Тут u- скорость движения вагона
Поскольку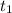 =
= 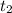 ,то
,то 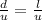 , откуда u =
, откуда u = 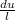
Определим значение искомой величины:
u= = 900м/с
= 900м/с
(:^)