Тіло масою 10 кг рухається під дією сили 50 Н.Визначте кінетичну енергію руху тіла через 2 с від початку руху. Відповідь дати у вигляді: число, пробіл, одиниця вимірювання
Против течения моторная лодка плывет медленнее чем в стоячей воде зато по течению быстрее. где удастся скорее проплыть одно и то же расстояние туда и обратно в реке или в озере
Если принять что моторная лодка плывет соскоростью V, а скорость течения реки U (причем скорость лодки больше скорости реки V>U или V/U > 1, так как если скорость реки больше или равна вернуться в исходную точку назад против течения не возможно). Примем что расстояние из одной точки в другую равно S Тогда вреня затраченное на путь туда и обратно в озере равно t1 = S/V+S/V= 2S/V Время затраченное на путь туда и обратно в реке равно t2 =S/(V-U) +S(V+U) = S*((V+U+V-U)/(V+U)(V-U)) =S*2V/(V^2-U^2)= = (2S/V)*(V^2/(V^2-U^2) = t1*(1/(1-(U/V)^2) Посмотрим на знаменатель дроби он равен 1-(U/V)^2 Величина 0< U/V <1 так как по условию V/U > 1 Следовательно 0< (U/V)^2 <1. Поэтому 0< 1-(U/V)^2 < 1. Следовательно 1/(1-(U/V)^2 >1 Поэтому t2 = t1*(1/(1-(U/V)^2) > t1 (доказано)
ответ: быстрее проплыть одно и тоже расстояние туда и обратно в озере.
7,095 мм.рт.ст. и 46% если измерения проводились психрометром Августа
8,741 мм.рт.ст. и 56% если измерения проводились психрометром Ассмана
Объяснение:
Психрометр Августа
Это классический психрометр, который мы знаем со школы. Абсолютную влажность для него найдем по формуле Реньо
где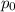
- давление насыщенных паров при температуре влажного термометра (в нашем случае 11,231 мм.рт.ст)
a - психрометрический коэффициент, для психрометра Августа равен 0,0011
B - текущее барометрическое давление
Проводим расчет
Относительная влажность
Психрометр Ассмана
Это психрометр с принудительным продувом воздуха.
Абсолютную влажность в данном случае рассчитаем по формуле Шпрунга (обозначения те же, что и в формуле Реньо)
Относительная влажность
Если принять что моторная лодка плывет соскоростью V, а скорость течения реки U
(причем скорость лодки больше скорости реки V>U или V/U > 1, так как если скорость реки больше или равна вернуться в исходную точку назад против течения не возможно).
Примем что расстояние из одной точки в другую равно S
Тогда вреня затраченное на путь туда и обратно в озере равно
t1 = S/V+S/V= 2S/V
Время затраченное на путь туда и обратно в реке равно
t2 =S/(V-U) +S(V+U) = S*((V+U+V-U)/(V+U)(V-U)) =S*2V/(V^2-U^2)=
= (2S/V)*(V^2/(V^2-U^2) = t1*(1/(1-(U/V)^2)
Посмотрим на знаменатель дроби он равен 1-(U/V)^2
Величина 0< U/V <1 так как по условию V/U > 1
Следовательно 0< (U/V)^2 <1. Поэтому 0< 1-(U/V)^2 < 1.
Следовательно 1/(1-(U/V)^2 >1
Поэтому t2 = t1*(1/(1-(U/V)^2) > t1 (доказано)
ответ: быстрее проплыть одно и тоже расстояние туда и обратно в озере.