В соответствии с законом Био-Савара бесконечный проводник на расстоянии r создает магнитное поле равное =.
Точка на бисектрисе на расстоянии 20 см от вершины расположена от проводников на расстоянии h=20см*sin(30)=10 см=0.1 м. То есть модуль вектора магнитной индукции для каждого проводника в точке равен Тл.
Суммарное магнитное поле будет равно сумме векторов в этой точке, причем это будет сумма векторов направленных под углом 120 градусов. Из геометрических построений модуль суммарного вектора оказывается равный каждому из векторов и равен
В соответствии с законом Био-Савара бесконечный проводник на расстоянии r создает магнитное поле равное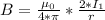 =
=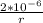 .
.
Точка на бисектрисе на расстоянии 20 см от вершины расположена от проводников на расстоянии h=20см*sin(30)=10 см=0.1 м. То есть модуль вектора магнитной индукции для каждого проводника в точке равен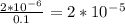 Тл.
Тл.
Суммарное магнитное поле будет равно сумме векторов в этой точке, причем это будет сумма векторов направленных под углом 120 градусов. Из геометрических построений модуль суммарного вектора оказывается равный каждому из векторов и равен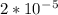
Раз мы ищем минимальный период, значит расстоянием от поверхности звезды до спутника можно пренебречь по сравнению с радиусом R самой звезды.
Сила притяжения равна центростремительной силе:
GMm/R² = mω²R, здесь М - масса звезды, а м - масса спутника. G - гравит. постоянная.
С учетом того, что круговая частота выражается через период:
ω = 2π/T,
а масса звезды выражается через плотность и объем:
M = ρ*V = (4πR³ρ)/3,
получим:
Gρ/3 = π/T²
Отсюда находим искомый минимальный период:
T = √[3π/(Gρ)] = √[3*3,14/(6,67*10^(-11) *10^17) ≈ 1,2*10^(-3) c = 1,2 мс