Тело массой 100г подвешенное на нити в течении одной минуты совершает гармонические колебания по закону х= 0,1 cos 3,14 t. Определить
период колебаний, частоту колебаний, число полных колебаний, амплитуду
колебаний, циклическую частоту, длину нити, максимальную скорость,
максимальное ускорение, максимальную силу действующую на тело, угол
отклонения нити от положения равновесия, высоту подъема тела. Построить
графики зависимость x(t), v(t), act ) и написать их уравнение колебания.
Определите ЧТО СМОЖЕТЕ
ответ: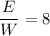
Объяснение:
Запишем уравнение гармонических колебаний в общем виде:
Будим считать, что маятник, в начальный момент времени, находился в положении максимального смещения от положения равновесия. В этом случае, когда мы отпустим маятник, он начнет совершать гармонические, незатухающие колебания.
Отсюда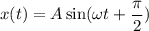 ⇒
⇒ 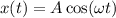 (1)
(1)
Мы знаем, что потенциальную энергию пружинного маятника W, в любой момент времени t, можно вычислить как kx²(t)/2, а кинетическую энергию E, как mv²(t)/2.
То-есть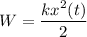 , но согласно уравнению (1) получим
, но согласно уравнению (1) получим 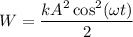
Аналогично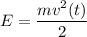 , однако мы знаем, что
, однако мы знаем, что 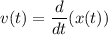
Тогда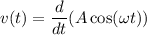 ⇒
⇒ 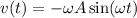 , а это значит что
, а это значит что 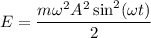
Поэтому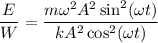 , так как
, так как 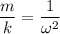 , то
, то 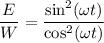 ⇒
⇒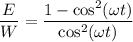 (2)
(2)
Теперь определим cos²(ωt), мы знаем, что в нашем случае, в момент момент времени t растяжение пружины маятника составило А/3, тогда согласно уравнению (1)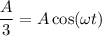 ⇒
⇒ 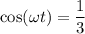 , следовательно
, следовательно 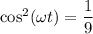
Возвращаясь к уравнению (2) получим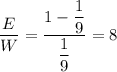
Система уравнений для равнозамедленного движения:
<
H(t) = U(0)t - gt^2/2,
U(t) = U(0) - gt.
>
Смотрим на уравнения и понимаем, что имеем 3 неизвестных, H, U(0), t,
убираем t:
H(t) = U(0)t - gt^2/2
g = U(0) - U(t)/t
H(t) = U(0)t - (U(0)-U(t))t/2
H(t) = (2U(0) + U(0) + U(t))t/2
H(t) = (U(0) + U(t)/2)t
t = U(0) - U(t)/g
H(t) = (U(0) - U(t))(U(0) + U(t))/2g
H(t) = U(0)^2 - U(t)^2/2g - формула пути при равнозамедленном движении, без времени.
{
Исходя из свойств параболы:
Hmax = U(0)^2/2g
}
Доказательство:
Наша функция H(t) выглядет вот так:
y = bx - ax^2
y/a = bx/a - x^2
y/a = - x^2 + 2bx/2a - b^2/4a^2 + b^2/4a^2
y/a = - (x - b/2a)^2 + b^2/4a^2
y = -a(x - b/2a)^2 + b^2/4a.
b^2/4a - минимальное/максимальное значение параболы, т.к. у = х + 5, где "5" двигает график вверх на 5.
Осталось подставить значение коэффициентов b и a нашего уравнения, тогда выражение примет вид:
U(0)^2/2g - это и будет максимальная высота полёта.
Hmax/ 2 = U(0)^2 - 100/2×10
U(0)^2/2×2×10 - 2U(0)^2/2×2×10 = - 100/2×10
- U(0)/ 2×2×10 = - 100/2×10
U(0) = 200 м/с
Hmax = 40000/200 = 200 м