Тонкая бесконечная нить согнута под углом 90°. Нить равномерно заряжена. На расстоянии 50 см от угла на продолжении одной из сторон расположен точечный заряд величиной 0,1 мкКл, на который со стороны нити действует сила 4,03 мН. Определить линейную плотность заряда нити

Показать ответ

Ответ:

ryzhij

15.10.2020 15:41

Посчитаем силу, действующую на этот заряд, обозначив его величину q, плотность заряда нити ρ, и расстояние до угла h

От участка нити, на продолжении которого она лежит посчитать просто, от каждого маленького участочка она действует в одном направлении

$\displaystyle\\F_1 = k\int\limits_h^\infty \frac{q\rho dx}{x^2} = q\rho(1/h - 1/\infty) = kq\rho/h$

От второго участка сложнее. Эта сила будет иметь проекцию как на направление вдоль первого участка, так и перпендикулярно ему.

Считаем первую

$\displaystyle\\F_{2(1)} = k\int_0^\infty \frac{q\rho}{h^2+x^2}\cos(\alpha(x))dx$

Здесь α(x) - угол между линией, соединяющией наш заряд и элемент второго участка нити dx, и самим вторым участком.

$\displaystyle\tan \alpha(x) = h/x\\d\alpha/\cos^2\alpha = -hdx/x^2\\dx = -\frac{hx^2d\alpha}{h^2\cos^2\alpha} = -\frac{hd\alpha}{\tan^2\alpha\cos^2\alpha} = -\frac{hd\alpha}{\sin^2\alpha}$

Меняем переменные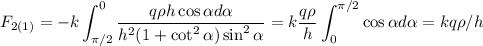 $\displaystyle\\F_{2(1)} = -k\int_{\pi/2}^{0}\frac{q\rho h\cos\alpha d\alpha}{h^2(1+\cot^2\alpha)\sin^2\alpha} = k\frac{q\rho}{h} \int_{0}^{\pi/2}\cos\alpha d\alpha = kq\rho/h$

Вторая компонента силы, перпендикулярная первой вычисляется почти тем же интегралом, только там вместо косинуса в числителе синус. Но значение интеграла от этого не меняется.

В итоге на зарядик действует сила 2kqρ/h вдоль продолжения одной из сторон и еще kqρ/h ей перпендикулярная. Итого

$\displaystyle\\F = \sqrt{5}kq\rho/h\\\rho = \frac{hF}{kq\sqrt{5}} \approx 1\mu Q/m$