В своей экспериментальной установке воспользуемся телом некоторой массы и наклонной плоскостью соответственно. Будем перемещать с силы F это тело с самого начала наклонной плоскости и до самого её конца, то есть до некоторой высоты h. Так же допустим, что у этой плоскости негладкая поверхность и коэффициент трения которой равен μ. То есть, на тело будет действовать сила трения Fтр.
Воспользуемся формулой для вычисления КПД наклонной плоскости.
КПД вычисляется по формуле:
Полезной работой будет являться сообщению телу потенциальной энергии, то есть:
где h - высота, м
g - ускорение свободного падения, 9.81 м / с ²
m - масса тела, кг
Затраченной работой будут работы совершённые силой F и Fтр, то есть:
( угол между линией перемещения и векторами сил равен нулю )
где F - сила, с которой тело перемещается на высоту h, H
Fтр - сила трения, действующая на тело, H
S - длина наклонной плоскости, м
Итого КПД получается равным:
Теперь рассмотрим саму наклонную плоскость. Конкретно нас интересует, как будет изменяться высота подъёма при изменении угла наклона плоскости. Длина наклонной плоскости остаётся постоянной ( S = const и следовательно Aз = const) .
Наклонная плоскость представляет собой прямоугольный треугольник, где d и h катеты треугольника и S гипотенуза треугольника ( ниже представлена схема) . Чтобы найти высоту наклонной плоскости, нужно длину наклонной плоскости умножить на синус угла α. То есть:
Допустим, что угол наклона нашей плоскости составляет 45°. Если мы будем увеличивать угол наклона, то получим, что значения градусной меры угла α будут увеличиваться и будут приближаться к значению 90°, где синус максимален и равен 1 ( sinα = 1 ) . Это можно проследить на тригонометрической окружности. Соответственно, исходя из равенства ( 2 ) заметим, что при увеличении угла до значений значений 45 < α < 90° увеличивается синус угла, и получается, что высота, на которую перемещается предмет, увеличивается. И наоборот, если будем брать значения угла 0 < α < 45, то высота, на которую будет перемещаться предмет будет уменьшаться. А это значит, что при изменении высоты, изменяется потенциальная энергия тела: при увеличении высоты h потенциальная энергия возрастает и соответственно КПД наклонной плоскости возрастает, а при уменьшении высоты h потенциальная энергия уменьшается и соответственно КПД наклонной плоскости уменьшается ( помним, что ) .
Таким образом угол наклона влияет на КПД наклонной плоскости.
Адронный коллайдер — это ускоритель заряженных частиц на встречных пучках, предназначенный для разгона протонов и тяжёлых ионов (ионов свинца) и изучения продуктов их соударений. Коллайдер построен в ЦЕРНе (Европейский совет ядерных исследований), находящемся около Женевы, на границе Швейцарии и Франции. БАК является самой крупной экспериментальной установкой в мире. В строительстве и исследованиях участвовали и участвуют более 10 тысяч учёных и инженеров более чем из 100 стран. Первостепенной задачей запуска коллайдера является подтверждение существования бозона Хиггса. Бозоны Хиггса – таинственный объект в последнем экспериментальном подтверждении.
Смотреть ниже.
Объяснение:
В своей экспериментальной установке воспользуемся телом некоторой массы и наклонной плоскостью соответственно. Будем перемещать с силы F это тело с самого начала наклонной плоскости и до самого её конца, то есть до некоторой высоты h. Так же допустим, что у этой плоскости негладкая поверхность и коэффициент трения которой равен μ. То есть, на тело будет действовать сила трения Fтр.
Воспользуемся формулой для вычисления КПД наклонной плоскости.
КПД вычисляется по формуле:
Полезной работой будет являться сообщению телу потенциальной энергии, то есть:
где h - высота, м
g - ускорение свободного падения, 9.81 м / с ²
m - масса тела, кг
Затраченной работой будут работы совершённые силой F и Fтр, то есть:
где F - сила, с которой тело перемещается на высоту h, H
Fтр - сила трения, действующая на тело, H
S - длина наклонной плоскости, м
Итого КПД получается равным:
Теперь рассмотрим саму наклонную плоскость. Конкретно нас интересует, как будет изменяться высота подъёма при изменении угла наклона плоскости. Длина наклонной плоскости остаётся постоянной ( S = const и следовательно Aз = const) .
Наклонная плоскость представляет собой прямоугольный треугольник, где d и h катеты треугольника и S гипотенуза треугольника ( ниже представлена схема) . Чтобы найти высоту наклонной плоскости, нужно длину наклонной плоскости умножить на синус угла α. То есть:
Допустим, что угол наклона нашей плоскости составляет 45°. Если мы будем увеличивать угол наклона, то получим, что значения градусной меры угла α будут увеличиваться и будут приближаться к значению 90°, где синус максимален и равен 1 ( sinα = 1 ) . Это можно проследить на тригонометрической окружности. Соответственно, исходя из равенства ( 2 ) заметим, что при увеличении угла до значений значений 45 < α < 90° увеличивается синус угла, и получается, что высота, на которую перемещается предмет, увеличивается. И наоборот, если будем брать значения угла 0 < α < 45, то высота, на которую будет перемещаться предмет будет уменьшаться. А это значит, что при изменении высоты, изменяется потенциальная энергия тела: при увеличении высоты h потенциальная энергия возрастает и соответственно КПД наклонной плоскости возрастает, а при уменьшении высоты h потенциальная энергия уменьшается и соответственно КПД наклонной плоскости уменьшается ( помним, что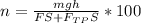 ) .
) .
Таким образом угол наклона влияет на КПД наклонной плоскости.
Адронный коллайдер — это ускоритель заряженных частиц на встречных пучках, предназначенный для разгона протонов и тяжёлых ионов (ионов свинца) и изучения продуктов их соударений. Коллайдер построен в ЦЕРНе (Европейский совет ядерных исследований), находящемся около Женевы, на границе Швейцарии и Франции. БАК является самой крупной экспериментальной установкой в мире. В строительстве и исследованиях участвовали и участвуют более 10 тысяч учёных и инженеров более чем из 100 стран. Первостепенной задачей запуска коллайдера является подтверждение существования бозона Хиггса. Бозоны Хиггса – таинственный объект в последнем экспериментальном подтверждении.