У кімнаті за температури 18 °С відносна вологість повітря 30 %. Скільки води треба додатково випаровувати для збільшення вологості до 60 %, якщо об єм кімнати - 50 м^2
B1. 1. сопротивление проводника -- увеличится 2. сила тока -- уменьшится 3. выделяющаяся на проводнике мощность -- уменьшится 1) Формула для элекрического сопротивления: Из формулы видно, что при увеличении длины в 2 раза - сопротивление тоже увеличится в 2 раза, эти величины прямопропорциональны. 2) По закону Ома сила тока определяется как Напряжение осталось тем же, сопротивление увеличилось, значит сила тока уменьшилась в 2 раза. 3) Мощность определяется как произведение силы тока и напряжения: Сила тока уменьшилась, значит и мощность уменьшилась (при постоянном напряжении).
В2. По закону Джоуля-Ленца количество теплоты, выделяющееся в проводнике с сопротивлением при прохождении через него тока за время определяется так: Воспользуемся законом Ома (), чтобы переписать закон Джоуля-Ленца через напряжение: При параллельном соединении напряжение на каждом из резисторов одинаковое (). Значит, количество выделенной теплоты будет определяться только в сопротивлением:
B3. Ом Закон Ома для полной цепи с наличием ЭДС: В первом случае имеем , а во втором . Приведем каждое из этих уравнений к общему знаменателю и получим систему двух уравнений на 2 неизвестных - и : Подставим известные величины из условия задачи и получим: Решением являются и .
В4. 3 А При последовательном соединении резисторов сила тока одинакова:
В5. 1.05 мКл (!) Решение по рисунку схемы в приложении (!). Емкость конденсатора определяется как . Отсюда, заряд конденсатора равен . Осталось только понять, какое напряжение на конденсаторе. Из рисунка видно, что конденсатор и резистор соединены параллельно, то есть . При этом ток через резистор равен полному току цепи, который можно определить по закону Ома для полной цепи: . Таким образом, можем найти напряжение на конденсаторе: . Теперь можем определить заряд на конденсаторе: Кл = 1.05 мКл
А1. 4) положительно заряженных частиц Это некоторая условность, физики просто так договорились.
А2. 4) 0,25 с По определению сила тока это кол-во заряда , перенесенного в единицу времени : Отсюда,
А3. 4) сила тока
А4. 2) 7 А (!) Всё зависит от таблицы. На просторах интернета я нашел такую таблицу (!) к этому заданию: U,В | 0 | 1 | 2 | 3 | 4 | 5 | I, А | 0 | 2 | 4 | 6 | 8 |10| Известно, что связь напряжения и силы тока - линейная и определяется по закону Ома: где - это сопротивление. Из таблицы видно, что Ом. Это справедливо для любой ячейки. Теперь осталось определить силу тока из закона Ома:
А5. 3) 500 м Формула для расчета сопротивления : Значит, длина провода определяется как Подставим числа из условия задачи Ом мм² = м² Ом·м и получим численное значение длины кабеля м = 500 м
А6. 1) уменьшится в 3 раза Начальное сопротивление проволоки . Сопротивление каждого из трех равных частей разрезанной пленки в соответствии с А5. Суммарное сопротивление при параллельном соединении определяется как В нашем случае, Перевернем дробь и получим, что . В итоге, сопротивление уменьшилось в раза.
А7. 1) = 12 A, = 4 A Резисторы соединены параллельно. Значит, напряжение на каждом из резисторов определяется одинаковое и равно 24 В: . Осталось только рассчитать силу тока на каждом резисторе по закону Ома для участка цепи:
А16. 1) 4 А Ток короткого замыкания определяется как где - это ЭДС, а - это внутреннее спортивление. Отсюда, можем найти ЭДС: . Теперь запишем закон Ома дя полной цепи: . Подставим ЭДС из условия короткого замыкания и получим: Осталось только произвести численные расчеты: .
B1.

 в 2 раза - сопротивление
в 2 раза - сопротивление  тоже увеличится в 2 раза, эти величины прямопропорциональны.
тоже увеличится в 2 раза, эти величины прямопропорциональны.

 определяется как произведение силы тока и напряжения:
определяется как произведение силы тока и напряжения:


 при прохождении через него тока
при прохождении через него тока  за время
за время  определяется так:
определяется так:
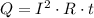
 ), чтобы переписать закон Джоуля-Ленца через напряжение:
), чтобы переписать закон Джоуля-Ленца через напряжение:

 ). Значит, количество выделенной теплоты будет определяться только в сопротивлением:
). Значит, количество выделенной теплоты будет определяться только в сопротивлением:

 Ом
Ом

 ,
,
 .
. и
и  :
:

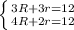
 и
и  .
.
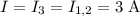
 определяется как
определяется как  . Отсюда, заряд конденсатора равен
. Отсюда, заряд конденсатора равен  . Осталось только понять, какое напряжение
. Осталось только понять, какое напряжение 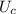 на конденсаторе. Из рисунка видно, что конденсатор и резистор
на конденсаторе. Из рисунка видно, что конденсатор и резистор 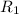 соединены параллельно, то есть
соединены параллельно, то есть  . При этом ток
. При этом ток  через резистор
через резистор 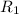 равен полному току цепи, который можно определить по закону Ома для полной цепи:
равен полному току цепи, который можно определить по закону Ома для полной цепи:
 .
.
 .
.
 Кл = 1.05 мКл
Кл = 1.05 мКл
1. сопротивление проводника -- увеличится
2. сила тока -- уменьшится
3. выделяющаяся на проводнике мощность -- уменьшится
1) Формула для элекрического сопротивления:
Из формулы видно, что при увеличении длины
2) По закону Ома сила тока определяется как
Напряжение осталось тем же, сопротивление увеличилось, значит сила тока уменьшилась в 2 раза.
3) Мощность
Сила тока уменьшилась, значит и мощность уменьшилась (при постоянном напряжении).
В2.
По закону Джоуля-Ленца количество теплоты, выделяющееся в проводнике с сопротивлением
Воспользуемся законом Ома (
При параллельном соединении напряжение на каждом из резисторов одинаковое (
B3.
Закон Ома для полной цепи с наличием ЭДС:
В первом случае имеем
а во втором
Приведем каждое из этих уравнений к общему знаменателю и получим систему двух уравнений на 2 неизвестных -
Подставим известные величины из условия задачи и получим:
Решением являются
В4. 3 А
При последовательном соединении резисторов сила тока одинакова:
В5. 1.05 мКл (!)
Решение по рисунку схемы в приложении (!).
Емкость конденсатора
Таким образом, можем найти напряжение на конденсаторе:
Теперь можем определить заряд на конденсаторе:
Это некоторая условность, физики просто так договорились.
А2. 4) 0,25 с
По определению сила тока
Отсюда,
А3. 4) сила тока
А4. 2) 7 А (!)
Всё зависит от таблицы. На просторах интернета я нашел такую таблицу (!) к этому заданию:
U,В | 0 | 1 | 2 | 3 | 4 | 5 |
I, А | 0 | 2 | 4 | 6 | 8 |10|
Известно, что связь напряжения
где
Из таблицы видно, что
А5. 3) 500 м
Формула для расчета сопротивления
Значит, длина провода определяется как
Подставим числа из условия задачи
и получим численное значение длины кабеля
А6. 1) уменьшится в 3 раза
Начальное сопротивление проволоки
Сопротивление каждого из трех равных частей разрезанной пленки
Суммарное сопротивление при параллельном соединении определяется как
В нашем случае,
Перевернем дробь и получим, что
В итоге, сопротивление уменьшилось в
А7. 1)
Резисторы соединены параллельно. Значит, напряжение на каждом из резисторов определяется одинаковое и равно 24 В:
Осталось только рассчитать силу тока на каждом резисторе по закону Ома для участка цепи:
А16. 1) 4 А
Ток короткого замыкания
где
Теперь запишем закон Ома дя полной цепи:
Подставим ЭДС из условия короткого замыкания и получим:
Осталось только произвести численные расчеты: