Для решения данной задачи воспользуемся понятием мгновенного центра скоростей. Если построить перпендикуляры к векторам и они пересекутся в точке Е, это и есть мгновенный центр скоростей, вся фигура вращается вокруг него с некоторой угловой скоростью ω. Найдем эту угловую скорость. Определим длину радиус вектора точки А - отрезка АЕ. Заметим, что угол ВАЕ - прямой, а угол ВАС при вершине треугольника 60°, таким образом, угол САЕ равен 30°. Из прямоугольного треугольника DAE имеем:
, где а - сторона треугольника.
Угловая скорость:
Теперь выразим расстояние ОЕ:
1) Скорость точки O:
м/с
2) Так как АЕ=ЕС, то и скорости точек А и С равны по модулю, т.е.:
В момент показанный на рисунке на два участка рамки действует сила Ампера. На участок ab (сила направлена на нас) и на участок cd (сила направлена от нас). Эти силы равны по модулю (токи одинаковые, поле одинаковое, длины одинаковые)
Собственно, направление этих сил не изменится и в дальнейшем. Будут еще возникать силы, действующие на горизонтальные участки рамки, но они не могут ее сдвинуть.
Так вот, две силы на ab и cd стремятся развернуть рамку перпендикулярно полю, чтобы ab было ближе к нам, а cd дальше от нас. В таком положении рамка могла бы покоится, потому что силы в данном положении ее только растягивают, но не крутят. Но когда это произойдет в нашей задаче, рамка наберет некоторую вращательную скорость и проскочит положение равновесия, и будет крутится дальше и в итоге повернется на 180 градусов. Затем две силы Ампера начнут крутить ее в другую сторону, и она снова проскочит положение равновесия и вернется в исходное положение. И так она и будет туда-сюда вращаться. Без затухания - вечно.
Дано:
АВ=ВС=АС;
__________
Найти: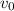 ,
, 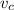
Для решения данной задачи воспользуемся понятием мгновенного центра скоростей. Если построить перпендикуляры к векторам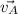 и
и 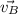 они пересекутся в точке Е, это и есть мгновенный центр скоростей, вся фигура вращается вокруг него с некоторой угловой скоростью ω. Найдем эту угловую скорость. Определим длину радиус вектора точки А - отрезка АЕ. Заметим, что угол ВАЕ - прямой, а угол ВАС при вершине треугольника 60°, таким образом, угол САЕ равен 30°. Из прямоугольного треугольника DAE имеем:
они пересекутся в точке Е, это и есть мгновенный центр скоростей, вся фигура вращается вокруг него с некоторой угловой скоростью ω. Найдем эту угловую скорость. Определим длину радиус вектора точки А - отрезка АЕ. Заметим, что угол ВАЕ - прямой, а угол ВАС при вершине треугольника 60°, таким образом, угол САЕ равен 30°. Из прямоугольного треугольника DAE имеем:
Угловая скорость:
Теперь выразим расстояние ОЕ:
1) Скорость точки O:
2) Так как АЕ=ЕС, то и скорости точек А и С равны по модулю, т.е.:
ответ: 1,2 м/с; 1,2 м/с.
В момент показанный на рисунке на два участка рамки действует сила Ампера. На участок ab (сила направлена на нас) и на участок cd (сила направлена от нас). Эти силы равны по модулю (токи одинаковые, поле одинаковое, длины одинаковые)
Собственно, направление этих сил не изменится и в дальнейшем. Будут еще возникать силы, действующие на горизонтальные участки рамки, но они не могут ее сдвинуть.
Так вот, две силы на ab и cd стремятся развернуть рамку перпендикулярно полю, чтобы ab было ближе к нам, а cd дальше от нас. В таком положении рамка могла бы покоится, потому что силы в данном положении ее только растягивают, но не крутят. Но когда это произойдет в нашей задаче, рамка наберет некоторую вращательную скорость и проскочит положение равновесия, и будет крутится дальше и в итоге повернется на 180 градусов. Затем две силы Ампера начнут крутить ее в другую сторону, и она снова проскочит положение равновесия и вернется в исходное положение. И так она и будет туда-сюда вращаться. Без затухания - вечно.