До включения ракетного двигателя модуль двигался как обычное тело, брошенное под углом к горизонту, расстояние от точки броска до наивысшей точки траектории определяется формулой
(1)
После включения двигателя, ускорение свободного падения уменьшилось на величину равную и стало составлять
(2)
Следовательно, новая дальность уже высчитывается для тела, брошенного горизонтально
(3)
Высоту полета h можно найти по формуле
(4)
Подставляя (4) в (3) и выполняя все преобразования, получим
Объяснение:
До включения ракетного двигателя модуль двигался как обычное тело, брошенное под углом к горизонту, расстояние от точки броска до наивысшей точки траектории определяется формулой
После включения двигателя, ускорение свободного падения уменьшилось на величину равную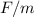 и стало составлять
и стало составлять
Следовательно, новая дальность уже высчитывается для тела, брошенного горизонтально
Высоту полета h можно найти по формуле
Подставляя (4) в (3) и выполняя все преобразования, получим
С учетом того, что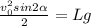 это следует из формулы (1)
это следует из формулы (1)
Или
1. Приступаючи до розв’язання задач з будь-якої теми, спочатку вивчіть
теоретичний матеріал за підручником, розберіться в прикладах розв’язання
типових задач.
2. Уважно прочитайте умову задачі, вникаючи в її зміст. Чітко уявіть
собі фізичне явище, процеси, які відображені умовою задачі.
3. Запишіть коротку умову задачі, вказуючи всі величини з умови
задачі та їх числові значення. Окремо позначте величини, що шукаються в
задачі. Числові значення переведіть в одиниці СІ.
4. Ретельно виконайте креслення, котре пояснює зміст задачі (в тих
випадках, коли це можливо). Є деякі задачі, що розв’язуються графічно, тоді
правильно виконане креслення буде розв’язанням задачі.
5. Згадайте, якому закону підпорядкований фізичний процес і якими
формулами він описується математично. Якщо формул декілька, співставте
величини, що входять у різні формули, із заданими величинами та тими, які
необхідно знайти.
6. На першому етапі розв’язуйте задачу в загальному вигляді, тобто
виводьте формулу, в котрій шукана величина виражена через величини,
задані в умові. Винятки із цього правила вкрай рідкі й бувають у двох
випадках: якщо формула якої-небудь проміжної величини настільки
громіздка, що обчислення цієї величини значно спрощує подальший запис
розв’язання; якщо числовий розв’язок задачі значно простіший, ніж
виведення формули.